【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族![]() 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当![]() 中
中![]() (
(![]() )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受![]() 影响,恒为
影响,恒为![]() 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:
(1)当![]() 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
(2)求该地上班族![]() 的人均通勤时间
的人均通勤时间![]() 的表达式;讨论
的表达式;讨论![]() 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
参考答案:
【答案】(1) ![]() 时,公交群体的人均通勤时间少于自驾群体的人均通勤时间;(2)见解析.
时,公交群体的人均通勤时间少于自驾群体的人均通勤时间;(2)见解析.
【解析】
(1)由题意知求出f(x)>40时x的取值范围即可;
(2)分段求出g(x)的解析式,判断g(x)的单调性,再说明其实际意义.
(1)由题意知,当![]() 时,
时,
![]() ,
,
即![]() ,
,
解得![]() 或
或![]() ,
,
∴![]() 时,公交群体的人均通勤时间少于自驾群体的人均通勤时间;
时,公交群体的人均通勤时间少于自驾群体的人均通勤时间;
(2)当![]() 时,
时,
![]() ;
;
当![]() 时,
时,
![]() ;
;
∴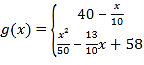 ;
;
当![]() 时,
时,![]() 单调递减;
单调递减;
当![]() 时,
时,![]() 单调递增;
单调递增;
说明该地上班族![]() 中有小于
中有小于![]() 的人自驾时,人均通勤时间是递减的;
的人自驾时,人均通勤时间是递减的;
有大于![]() 的人自驾时,人均通勤时间是递增的;
的人自驾时,人均通勤时间是递增的;
当自驾人数为![]() 时,人均通勤时间最少.
时,人均通勤时间最少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过随机询问72名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
男
女
总计
读营养说明
16
28
44
不读营养说明
20
8
28
总计
36
36
72
(1)根据以上列联表判断,能否在犯错误的概率不超过0.005的前提下认为性别和是否看营养说明有关系呢?
(2)从被询问的28名不读营养说明的大学生中,随机抽取2名学生,求抽到女生人数
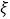
的分布列及数学期望.
附:
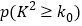
0.010
0.005
0.001
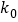
6.635
7.879
10.828
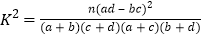
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=
 (|x﹣a2|+|x﹣2a2|﹣3a2),若x∈R,f(x﹣1)≤f(x),则实数a的取值范围为( )
(|x﹣a2|+|x﹣2a2|﹣3a2),若x∈R,f(x﹣1)≤f(x),则实数a的取值范围为( )
A.[﹣ ,
,  ]
]
B.[﹣ ,
,  ]
]
C.[﹣ ,
,  ]
]
D.[﹣ ,
,  ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系
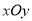 的原点,极轴为
的原点,极轴为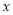 轴的正半轴,两种坐标系中的长度单位相同,已知曲线
轴的正半轴,两种坐标系中的长度单位相同,已知曲线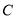 的极坐标方程为
的极坐标方程为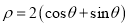 .
.(1)求
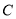 的直角坐标方程;
的直角坐标方程;(2)直线
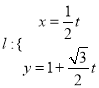 (
(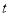 为参数)与曲线
为参数)与曲线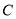 交于
交于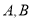 两点,与
两点,与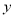 轴交于
轴交于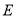 ,求
,求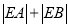 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a是一个各位数字都不是0且没有重复数字三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=815,则I(a)=158,D(a)=851),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
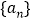 为等差数列,
为等差数列,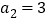 ,
,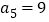 .
.(1) 求数列
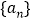 的通项公式;
的通项公式;(2)求数列
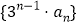 的前n项和
的前n项和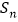 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:
f(t)=10﹣ ,t∈[0,24)
,t∈[0,24)
(1)求实验室这一天的最大温差;
(2)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温?
相关试题

