【题目】某实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:
f(t)=10﹣ ![]() ,t∈[0,24)
,t∈[0,24)
(1)求实验室这一天的最大温差;
(2)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温?
参考答案:
【答案】
(1)解:∵f(t)=10﹣ ![]() =10﹣2sin(
=10﹣2sin( ![]() t+
t+ ![]() ),t∈[0,24),
),t∈[0,24),
∴ ![]() ≤
≤ ![]() t+
t+ ![]() <
< ![]() ,故当
,故当 ![]() t+
t+ ![]() =
= ![]() 时,及t=14时,函数取得最大值为10+2=12,
时,及t=14时,函数取得最大值为10+2=12,
当 ![]() t+
t+ ![]() =
= ![]() 时,即t=2时,函数取得最小值为10﹣2=8,
时,即t=2时,函数取得最小值为10﹣2=8,
故实验室这一天的最大温差为12﹣8=4℃.
(2)解:由题意可得,当f(t)>11时,需要降温,由(Ⅰ)可得f(t)=10﹣2sin( ![]() t+
t+ ![]() ),
),
由10﹣2sin( ![]() t+
t+ ![]() )>11,求得sin(
)>11,求得sin( ![]() t+
t+ ![]() )<﹣
)<﹣ ![]() ,即
,即 ![]() <
< ![]() t+
t+ ![]() <
< ![]() ,
,
解得10<t<18,即在10时到18时,需要降温.
【解析】(1)利用两角和差的正弦公式化简函数解析式为f(t)10﹣2sin( ![]() t+
t+ ![]() ),t∈[0,24),利用正弦函数的定义域和值域求得f(x)的最大值及最小值,可得实验室这一天的最大温差.(2)由题意可得,当f(t)>11时,需要降温,由f(t)>11,求得sin(
),t∈[0,24),利用正弦函数的定义域和值域求得f(x)的最大值及最小值,可得实验室这一天的最大温差.(2)由题意可得,当f(t)>11时,需要降温,由f(t)>11,求得sin( ![]() t+
t+ ![]() )<﹣
)<﹣ ![]() ,即
,即 ![]() <
< ![]() t+
t+ ![]() <
< ![]() ,解得t的范围,可得结论.
,解得t的范围,可得结论.
【考点精析】掌握函数y=Asin(ωx+φ)的图象变换是解答本题的根本,需要知道图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族
 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当 中
中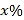 (
( )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受 影响,恒为
影响,恒为 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:(1)当
 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?(2)求该地上班族
 的人均通勤时间
的人均通勤时间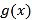 的表达式;讨论
的表达式;讨论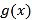 的单调性,并说明其实际意义.
的单调性,并说明其实际意义. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a是一个各位数字都不是0且没有重复数字三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=815,则I(a)=158,D(a)=851),阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
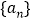 为等差数列,
为等差数列,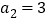 ,
,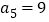 .
.(1) 求数列
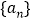 的通项公式;
的通项公式;(2)求数列
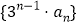 的前n项和
的前n项和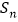 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,若
,若 ,
, 时,有
时,有 成立.
成立.(1)判断
 在
在 上的单调性,并证明;
上的单调性,并证明;(2)解不等式:
 ;
;(3)若
 对所有的
对所有的 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, 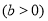 ,在
,在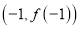 处的切线方程为
处的切线方程为 .
.(1)求
 ,
,  ;
;(2)若
 ,证明:
,证明:  .
.【答案】(1)
 ,
,  ;(2)见解析
;(2)见解析【解析】试题分析:(1)求出函数的导数,得到关于
 的方程组,解出即可;
的方程组,解出即可;(2)由(1)可知
 ,
,  ,
,由
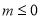 ,可得
,可得 ,令
,令 , 利用导数研究其单调性可得
, 利用导数研究其单调性可得 ,
,从而证明
 .
.试题解析:((1)由题意
 ,所以
,所以 ,
,又
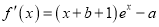 ,所以
,所以 ,
, 若
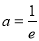 ,则
,则 ,与
,与 矛盾,故
矛盾,故 ,
,  .
.(2)由(1)可知
 ,
,  ,
,由
 ,可得
,可得 ,
,令
 ,
,  ,
,令

当
 时,
时,  ,
,  单调递减,且
单调递减,且 ;
;当
 时,
时,  ,
,  单调递增;且
单调递增;且 ,
,所以
 在
在 上当单调递减,在
上当单调递减,在 上单调递增,且
上单调递增,且 ,
,故
 ,
,故
 .
.【点睛】本题考查利用函数的切线求参数的方法,以及利用导数证明不等式的方法,解题时要认真审题,注意导数性质的合理运用.
【题型】解答题
【结束】
22【题目】在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( ,
,  为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,  轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 ,若直线
,若直线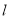 与曲线
与曲线 相切;
相切;(1)求曲线
 的极坐标方程;
的极坐标方程;(2)在曲线
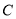 上取两点
上取两点 ,
,  与原点
与原点 构成
构成 ,且满足
,且满足 ,求面积
,求面积 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1的参数方程是
 (θ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=-2cosθ.
(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=-2cosθ.(1)写出C1的极坐标方程和C2的直角坐标方程;
(2)已知点M1、M2的极坐标分别是(1,π)、(2,
 ),直线M1M2与曲线C2相交于P、Q两点,射线OP与曲线C1相交于点A,射线OQ与曲线C1相交于点B,求
),直线M1M2与曲线C2相交于P、Q两点,射线OP与曲线C1相交于点A,射线OQ与曲线C1相交于点B,求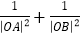 的值.
的值.
相关试题

