【题目】通过随机询问72名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
男 | 女 | 总计 | ||
读营养说明 | 16 | 28 | 44 | |
不读营养说明 | 20 | 8 | 28 | |
总计 | 36 | 36 | 72 |
(1)根据以上列联表判断,能否在犯错误的概率不超过0.005的前提下认为性别和是否看营养说明有关系呢?
(2)从被询问的28名不读营养说明的大学生中,随机抽取2名学生,求抽到女生人数![]()
的分布列及数学期望.
附:
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
![]()
参考答案:
【答案】(1) 能(2)分布列见解析,期望为![]() .
.
【解析】分析:(1)根据所给数据与公式计算![]() ,可得结论;
,可得结论;
(2)![]() 的取值分别为
的取值分别为![]() ,根据超几何分布计算出名概率,可得分布列,再由期望公式可计算出期望.
,根据超几何分布计算出名概率,可得分布列,再由期望公式可计算出期望.
详解:(1)由计算可得![]() 的观测值为
的观测值为![]() .
.
因为![]() ,而
,而![]() ,
,
所以在犯错误的概率不超过0.005的前提下认为“性别与读营养说明之间有关系”.
(2)![]() 的取值为0,1,2.
的取值为0,1,2.
![]() ,
,![]() ,
,![]() .
.
![]() 的分布列为
的分布列为
| 0 | 1 | 2 |
|
|
|
|
数学期望为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱柱
 中,点
中,点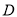 是
是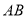 的中点.
的中点.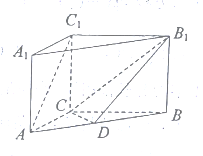
(1)求证:
 平面
平面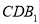 ;
;(2)若
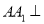 平面
平面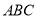 ,
, 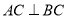 ,
, 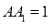 ,
, 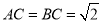 ,求二面角
,求二面角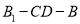 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
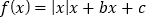 ,则下列命题中正确的个数是( )
,则下列命题中正确的个数是( )①当
 时,函数
时,函数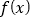 在
在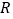 上是单调增函数;
上是单调增函数;②当
 时,函数
时,函数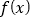 在
在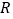 上有最小值;
上有最小值;③函数
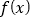 的图象关于点
的图象关于点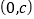 对称;
对称;④方程
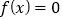 可能有三个实数根.
可能有三个实数根.A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】从甲地到乙地要经过3个十字路口,设各路口信号灯工作相互独立,且在各路口遇到红灯的概率分别为
 .
.(Ⅰ)设
 表示一辆车从甲地到乙地遇到红灯的个数,求随机变量
表示一辆车从甲地到乙地遇到红灯的个数,求随机变量 的分布列和数学期望;
的分布列和数学期望;(Ⅱ)若有2辆车独立地从甲地到乙地,求这2辆车共遇到1个红灯的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)是定义在R上的奇函数,当x≥0时,f(x)=
 (|x﹣a2|+|x﹣2a2|﹣3a2),若x∈R,f(x﹣1)≤f(x),则实数a的取值范围为( )
(|x﹣a2|+|x﹣2a2|﹣3a2),若x∈R,f(x﹣1)≤f(x),则实数a的取值范围为( )
A.[﹣ ,
,  ]
]
B.[﹣ ,
,  ]
]
C.[﹣ ,
,  ]
]
D.[﹣ ,
,  ]
] -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
极坐标系的极点为直角坐标系
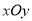 的原点,极轴为
的原点,极轴为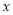 轴的正半轴,两种坐标系中的长度单位相同,已知曲线
轴的正半轴,两种坐标系中的长度单位相同,已知曲线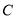 的极坐标方程为
的极坐标方程为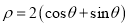 .
.(1)求
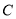 的直角坐标方程;
的直角坐标方程;(2)直线
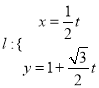 (
(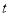 为参数)与曲线
为参数)与曲线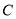 交于
交于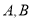 两点,与
两点,与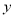 轴交于
轴交于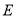 ,求
,求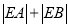 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某群体的人均通勤时间,是指单日内该群体中成员从居住地到工作地的平均用时.某地上班族
 中的成员仅以自驾或公交方式通勤.分析显示:当
中的成员仅以自驾或公交方式通勤.分析显示:当 中
中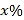 (
( )的成员自驾时,自驾群体的人均通勤时间为
)的成员自驾时,自驾群体的人均通勤时间为 (单位:分钟),而公交群体的人均通勤时间不受
(单位:分钟),而公交群体的人均通勤时间不受 影响,恒为
影响,恒为 分钟,试根据上述分析结果回答下列问题:
分钟,试根据上述分析结果回答下列问题:(1)当
 在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?
在什么范围内时,公交群体的人均通勤时间少于自驾群体的人均通勤时间?(2)求该地上班族
 的人均通勤时间
的人均通勤时间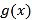 的表达式;讨论
的表达式;讨论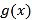 的单调性,并说明其实际意义.
的单调性,并说明其实际意义.
相关试题

