【题目】△ABC中,角A,B,C的对边分别为a,b,c,且2bcosC+c=2a.
(Ⅰ)求角B的大小;
(Ⅱ)若![]() ,求
,求![]() 的值.
的值.
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)由于2bcosC+c=2a,是关于边的一次齐次式,所以用正弦定理把边化为角,可得到![]() ,
,![]() 。(2)由(1)中
。(2)由(1)中![]() 和
和![]() ,可知A,B角己知,同时根据三角形内角为
,可知A,B角己知,同时根据三角形内角为![]() ,也可以sinC,所以
,也可以sinC,所以![]() ,可解。
,可解。
试题解析:(Ⅰ)在△ABC中,∵2bcosC+c=2a,
由正弦定理,得2sinBcosC+sinC=2sinA,
∵A+B+C=π,
∴sinA=sin(B+C)=sinBcosC+cosBsinC,…
∴2sinBcosC+sinC=2(sinBcosC+cosBsinC),
∴sinC=2cosBsinC,
∵0<C<π,∴sinC≠0,
∴![]() ,
,
∵0<B<π,∴![]() .
.
(Ⅱ)∵三角形ABC中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x
2011
2012
2013
2014
2015
储蓄存款y(千亿元)
5
6
7
8
10
为了研究计算的方便,工作人员将上表的数据进行了处理,
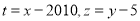 得到下表2:
得到下表2:时间代号t
1
2
3
4
5
z
0
1
2
3
5
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出y关于x的回归方程;
(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程
 ,其中
,其中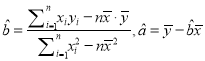 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
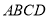 中,
中, 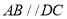 ,
, 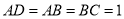 ,
, 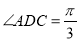 ,平面
,平面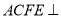 平面
平面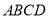 ,四边形
,四边形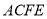 是矩形,
是矩形, 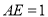 ,点
,点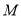 在线段
在线段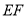 上.
上.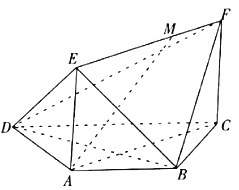
(1)当
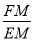 为何值时,
为何值时, 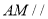 平面
平面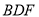 ?证明你的结论;
?证明你的结论;(2)求二面角
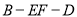 的平面角的余弦值.
的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于95为正品,小于95为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标


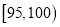
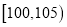
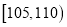
机床甲
8
12
40
32
8
机床乙
7
18
40
29
6
(1)试分别估计甲机床、乙机床生产的零件为正品的概率;
(2)甲机床生产一件零件,若是正品可盈利160元,次品则亏损20元;乙机床生产一件零件,若是正品可盈利200元,次品则亏损40元,在(1)的前提下,现需生产这种零件2件,以获得利润的期望值为决策依据,应该如何安排生产最佳?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 的圆心在坐标原点,且与直线
的圆心在坐标原点,且与直线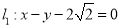 相切.
相切.(1)求直线
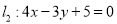 被圆
被圆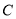 所截得的弦
所截得的弦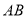 的长;
的长;(2)过点
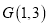 作两条与圆
作两条与圆 相切的直线,切点分别为
相切的直线,切点分别为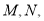 求直线
求直线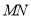 的方程;
的方程;(3)若与直线
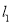 垂直的直线
垂直的直线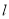 与圆
与圆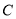 交于不同的两点
交于不同的两点 ,若
,若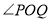 为钝角,求直线
为钝角,求直线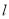 在
在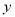 轴上的截距的取值范围.
轴上的截距的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
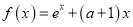 (其中
(其中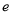 为自然对数的底数)
为自然对数的底数)(1)设过点
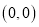 的直线
的直线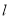 与曲线
与曲线 相切于点
相切于点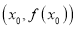 ,求
,求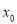 的值;
的值;(2)若函数
 的图象与函数
的图象与函数 的图象在
的图象在 内有交点,求实数
内有交点,求实数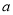 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是斜三角形,内角A、B、C所对的边的长分别为a、b、c.若csinA=
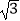 acosC.
acosC.
(1)求角C;
(2)若c=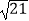 ,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
相关试题

