【题目】已知圆![]() 的圆心在坐标原点,且与直线
的圆心在坐标原点,且与直线![]() 相切.
相切.
(1)求直线![]() 被圆
被圆![]() 所截得的弦
所截得的弦![]() 的长;
的长;
(2)过点![]() 作两条与圆
作两条与圆![]() 相切的直线,切点分别为
相切的直线,切点分别为![]() 求直线
求直线![]() 的方程;
的方程;
(3)若与直线![]() 垂直的直线
垂直的直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,若
,若![]() 为钝角,求直线
为钝角,求直线![]() 在
在![]() 轴上的截距的取值范围.
轴上的截距的取值范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,且
,且![]() .
.
【解析】【试题分析】(1)依据题设先求圆的半径和方程,再运用弦心距、半弦长、半径之间的关系进行分析求解;(2)依据题设条件构造圆以![]() 的方程,再运用两圆的相交弦所在直线即为所求;(3)依据题设条件借助题设条件“
的方程,再运用两圆的相交弦所在直线即为所求;(3)依据题设条件借助题设条件“![]() 为钝角”建立不等式分析探求:
为钝角”建立不等式分析探求:
(1)由题意得:圆心![]() 到直线
到直线![]() 的距离为圆的半径,
的距离为圆的半径,
![]() ,所以圆
,所以圆![]() 的标准方程为:
的标准方程为: ![]()
所以圆心到直线![]() 的距离
的距离![]()
![]()
![]()
(2)因为点![]() ,所以
,所以![]() ,
,![]()
所以以![]() 点为圆心,线段
点为圆心,线段![]() 长为半径的圆
长为半径的圆![]() 方程:
方程: ![]() (1)
(1)
又圆![]() 方程为:
方程为: ![]() (2),由
(2),由![]() 得直线
得直线![]() 方程:
方程: ![]()
(3)设直线![]() 的方程为:
的方程为: ![]() 联立
联立![]() 得:
得: ![]() ,
,
设直线![]() 与圆的交点
与圆的交点![]() ,
,
由![]() ,得
,得![]() ,
, ![]() (3)
(3)
因为![]() 为钝角,所以
为钝角,所以![]() ,
,
即满足![]() ,且
,且![]() 与
与![]() 不是反向共线,
不是反向共线,
又![]() ,所以
,所以![]() (4)
(4)
由(3)(4)得![]() ,满足
,满足![]() ,即
,即![]() ,
,
当![]() 与
与![]() 反向共线时,直线
反向共线时,直线![]() 过原点,此时
过原点,此时![]() ,不满足题意,
,不满足题意,
故直线![]() 在
在![]() 轴上的截距的取值范围是
轴上的截距的取值范围是![]() ,且
,且![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
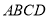 中,
中, 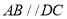 ,
, 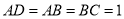 ,
, 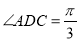 ,平面
,平面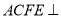 平面
平面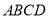 ,四边形
,四边形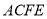 是矩形,
是矩形, 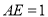 ,点
,点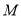 在线段
在线段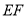 上.
上.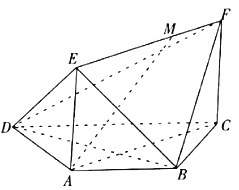
(1)当
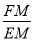 为何值时,
为何值时, 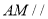 平面
平面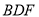 ?证明你的结论;
?证明你的结论;(2)求二面角
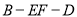 的平面角的余弦值.
的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于95为正品,小于95为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标


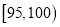
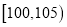
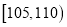
机床甲
8
12
40
32
8
机床乙
7
18
40
29
6
(1)试分别估计甲机床、乙机床生产的零件为正品的概率;
(2)甲机床生产一件零件,若是正品可盈利160元,次品则亏损20元;乙机床生产一件零件,若是正品可盈利200元,次品则亏损40元,在(1)的前提下,现需生产这种零件2件,以获得利润的期望值为决策依据,应该如何安排生产最佳?
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,角A,B,C的对边分别为a,b,c,且2bcosC+c=2a.
(Ⅰ)求角B的大小;
(Ⅱ)若
 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
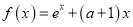 (其中
(其中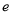 为自然对数的底数)
为自然对数的底数)(1)设过点
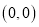 的直线
的直线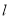 与曲线
与曲线 相切于点
相切于点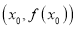 ,求
,求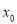 的值;
的值;(2)若函数
 的图象与函数
的图象与函数 的图象在
的图象在 内有交点,求实数
内有交点,求实数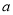 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC是斜三角形,内角A、B、C所对的边的长分别为a、b、c.若csinA=
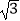 acosC.
acosC.
(1)求角C;
(2)若c=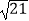 ,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
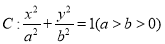 短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为
短轴端点和两个焦点的连线构成正方形,且该正方形的内切圆方程为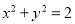 .
. (1)求椭圆
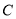 的方程;
的方程;(2)若抛物线
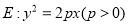 的焦点与椭圆
的焦点与椭圆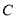 的一个焦点
的一个焦点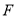 重合,直线
重合,直线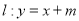 与抛物线
与抛物线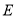 交于两点
交于两点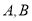 ,且
,且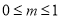 ,求
,求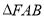 的面积的最大值.
的面积的最大值.
相关试题

