【题目】某地随着经济的发展,居民收入逐年增长,下表是该地一建设银行连续五年的储蓄存款(年底余额),如下表1:
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
储蓄存款y(千亿元) | 5 | 6 | 7 | 8 | 10 |
为了研究计算的方便,工作人员将上表的数据进行了处理, ![]() 得到下表2:
得到下表2:
时间代号t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(Ⅰ)求z关于t的线性回归方程;
(Ⅱ)通过(Ⅰ)中的方程,求出y关于x的回归方程;
(Ⅲ)用所求回归方程预测到2020年年底,该地储蓄存款额可达多少?
(附:对于线性回归方程![]() ,其中
,其中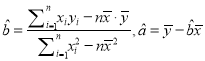 )
)
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)15.6千亿元
(3)15.6千亿元
【解析】试题分析:(Ⅰ)先分别求出![]() ,再代入公式
,再代入公式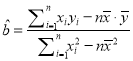 得
得![]() ,因此
,因此![]() ,从而线性回归方程为
,从而线性回归方程为![]() (Ⅱ)将
(Ⅱ)将![]() 代入(1)中方程
代入(1)中方程![]() ,化简得
,化简得![]() (Ⅲ)即求自变量为2020时的函数值:
(Ⅲ)即求自变量为2020时的函数值: ![]()
试题解析:解:(1)![]()
![]()
![]()
![]() ,
, ![]()
![]()
(2)![]() ,代入
,代入![]() 得到:
得到:
![]() ,即
,即![]()
(3)![]() ,
,
![]() 预测到2020年年底,该地储蓄存款额可达15.6千亿元
预测到2020年年底,该地储蓄存款额可达15.6千亿元
-
科目: 来源: 题型:
查看答案和解析>>【题目】若数列{an}的前n项和Sn满足Sn=2an+n.
(Ⅰ)求证:数列{an﹣1}是等比数列;
(Ⅱ)记bn=
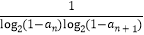 ,求数列{bn}的前n项和.
,求数列{bn}的前n项和. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 是圆
是圆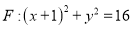 上的任意一点,点
上的任意一点,点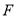 为圆
为圆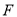 的圆心,点
的圆心,点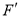 与点
与点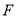 关于平面直角系的坐标原点对称,线段
关于平面直角系的坐标原点对称,线段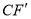 的垂直平分线与线段
的垂直平分线与线段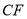 交于点
交于点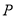 .
.(1)求动点
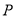 的轨迹
的轨迹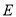 的方程;
的方程;(2)若轨迹
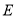 与
与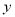 轴正半轴交于点
轴正半轴交于点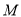 ,直线
,直线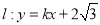 交轨迹
交轨迹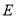 于
于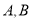 两点,求
两点,求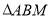 面积的取值范围.
面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高产品的年产量,某企业拟在2013年进行技术改革,经调查测算,产品当年的产量x万件与投入技术改革费用m万元(m≥0)满足x=3﹣
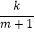 (k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产均能销售出去,厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金)
(k为常数).如果不搞技术改革,则该产品当年的产量只能是1万件.已知2013年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元.由于市场行情较好,厂家生产均能销售出去,厂家将每件产品的销售价格定为每件产品生产成本的1.5倍(生产成本包括固定投入和再投入两部分资金)
(1)试确定k的值,并将2013年该产品的利润y万元表示为技术改革费用m万元的函数(利润=销售金额﹣生产成本﹣技术改革费用);
(2)该企业2013年的技术改革费用投入多少万元时,厂家的利润最大?并求出最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形
 中,
中, 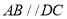 ,
, 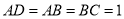 ,
, 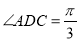 ,平面
,平面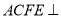 平面
平面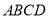 ,四边形
,四边形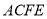 是矩形,
是矩形, 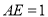 ,点
,点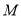 在线段
在线段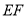 上.
上.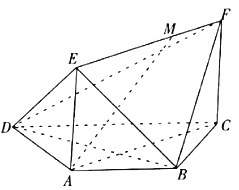
(1)当
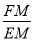 为何值时,
为何值时, 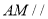 平面
平面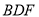 ?证明你的结论;
?证明你的结论;(2)求二面角
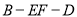 的平面角的余弦值.
的平面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于95为正品,小于95为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标


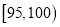
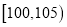
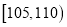
机床甲
8
12
40
32
8
机床乙
7
18
40
29
6
(1)试分别估计甲机床、乙机床生产的零件为正品的概率;
(2)甲机床生产一件零件,若是正品可盈利160元,次品则亏损20元;乙机床生产一件零件,若是正品可盈利200元,次品则亏损40元,在(1)的前提下,现需生产这种零件2件,以获得利润的期望值为决策依据,应该如何安排生产最佳?
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,角A,B,C的对边分别为a,b,c,且2bcosC+c=2a.
(Ⅰ)求角B的大小;
(Ⅱ)若
 ,求
,求 的值.
的值.
相关试题

