【题目】
某园艺公司种植了一批名贵树苗,为了解树苗的生长情况,从这批树苗中随机地测量了![]() 棵树苗的高度(单位:厘米),并把这些高度列成如下的频数分布表:
棵树苗的高度(单位:厘米),并把这些高度列成如下的频数分布表:
组别 |
|
|
|
|
|
|
频数 | 2 | 4 | 11 | 16 | 13 | 4 |
(Ⅰ)在这批树苗中任取一棵,其高度在![]() 厘米以上的概率大约是多少?这批树苗的平均高度大约是多少?
厘米以上的概率大约是多少?这批树苗的平均高度大约是多少?
(Ⅱ)为了进一步获得研究资料,标记![]() 组中的树苗为
组中的树苗为![]() ,
,![]() 组中的树苗为
组中的树苗为![]() ,现从
,现从![]() 组中移出一棵树苗,从
组中移出一棵树苗,从![]() 组中移出两棵树苗进行试验研究,则
组中移出两棵树苗进行试验研究,则![]() 组的树苗
组的树苗![]() 和
和![]() 组的树苗
组的树苗![]() 同时被移出的概率是多少?
同时被移出的概率是多少?
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(Ⅰ)根据题意,由频率分布表可得高度不低于80厘米的频数,进而由等可能事件的概率公式,计算可得答案;
(Ⅱ)设![]() 组中的树苗为
组中的树苗为![]() 组中的树苗为
组中的树苗为![]() 用列表法可得移出1棵树苗的基本事件的数目与
用列表法可得移出1棵树苗的基本事件的数目与![]() 同时被移出的事件数目,由等可能事件的概率公式计算可得答案.
同时被移出的事件数目,由等可能事件的概率公式计算可得答案.
试题解析:(Ⅰ)在这批树苗中任取一棵,其高度在![]() 厘米以上的概率大约是
厘米以上的概率大约是![]()
这批树苗的平均高度大约是
![]() (cm)
(cm)
(Ⅱ)从![]() 组中移出一棵树苗,从
组中移出一棵树苗,从![]() 组中移出两棵树苗的所有可能为ACD,ACE,ACF,ADE,ADF,AEF,BCD,BCE,BCF,BDE,BDF,BEF共12种,
组中移出两棵树苗的所有可能为ACD,ACE,ACF,ADE,ADF,AEF,BCD,BCE,BCF,BDE,BDF,BEF共12种,
其中![]() 组的树苗
组的树苗![]() 和
和![]() 组的树苗
组的树苗![]() 同时被移出的可能为ACD,ACE,ACF,共3种.
同时被移出的可能为ACD,ACE,ACF,共3种.
设![]() 组的树苗
组的树苗![]() 和
和![]() 组的树苗
组的树苗![]() 同时被移出为事件M,
同时被移出为事件M,
则![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC的内角A、B、C所对的边分别为a,b,c. (Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);
(Ⅱ)若a,b,c成等比数列,且c=2a,求cosB的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
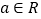 ,函数
,函数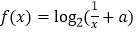 .
.(1)当
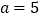 时,解不等式
时,解不等式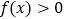 ;
;(2)若关于
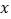 的方程
的方程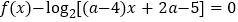 的解集中恰好有一个元素,求
的解集中恰好有一个元素,求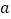 的取值范围;
的取值范围;(3)设
 ,若对任意
,若对任意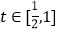 ,函数
,函数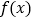 在区间
在区间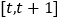 上的最大值与最小值的差不超过1,求
上的最大值与最小值的差不超过1,求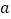 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】第十三届全运会将在2017年8月在天津举行,组委会在2017年1月对参加接待服务的10名宾馆经理进行为期半月的培训,培训结束,组织了一次培训结业测试,10人考试成绩如下(满分为100分):
75 84 65 90 88 95 78 85 98 82
(Ⅰ)以成绩的十位为茎个位为叶作出本次结业成绩的茎叶图,并计算平均成绩与成绩中位数 ;
(Ⅱ)从本次结业成绩在80分以上的人员中选3人,这3人中成绩在90分(含90分)以上的人数为
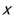 ,求
,求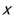 的分布列与数学期望.
的分布列与数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的不等式ax2+(1﹣a)x﹣1>0
(1)当a=2时,求不等式的解集.
(2)当a>﹣1时.求不等式的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】设△ABC的内角A,B,C所对的边分别为a,b,c且acosC﹣
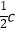 =b.
=b.
(1)求角A的大小;
(2)若a=1,求△ABC的周长的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(第x周)和市场占有率(y﹪)的几组相关数据如下表:

1
2
3
4
5

0.03
0.06
0.1
0.14
0.17
(Ⅰ)根据表中的数据,用最小二乘法求出
 关于
关于 的线性回归方程
的线性回归方程 ;
;(Ⅱ)根据上述线性回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测在第几周,该款旗舰机型市场占有率将首次超过 0.40﹪(最后结果精确到整数).
参考公式:
 ,
,
相关试题

