【题目】如图,已知直四棱柱![]() 的底面是直角梯形,
的底面是直角梯形,![]() ,
,![]() ,
,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 上的动点,且
上的动点,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
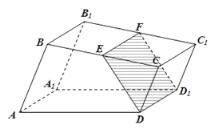
(1)证明:无论点![]() 怎样运动,四边形
怎样运动,四边形![]() 都为矩形;
都为矩形;
(2)当![]() 时,求几何体
时,求几何体![]() 的体积.
的体积.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用面面平行的性质定理得出![]() ,由面面平行的性质定理可得出
,由面面平行的性质定理可得出![]() ,可证明出四边形
,可证明出四边形![]() 为平行四边形,由
为平行四边形,由![]() 平面
平面![]() ,可得出
,可得出![]() ,从而可证明出四边形
,从而可证明出四边形![]() 为矩形;
为矩形;
(2)计算出梯形![]() 的面积和
的面积和![]() 的面积,将梯形
的面积,将梯形![]() 的面积减去
的面积减去![]() 的面积可得出四边形
的面积可得出四边形![]() 的面积,再利用柱体的体积公式可求出几何体
的面积,再利用柱体的体积公式可求出几何体![]() 的体积.
的体积.
(1)在直四棱柱![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() .
.
在直四棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
在直四棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,
因此,无论点![]() 怎样运动,四边形
怎样运动,四边形![]() 都为矩形;
都为矩形;
(2)由于四边形![]() 是直角梯形,且
是直角梯形,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以,梯形![]() 的面积为
的面积为![]() ,
,
![]() ,易得
,易得![]() ,
,![]() 的面积为
的面积为![]() ,
,
![]() 四边形
四边形![]() 的面积为
的面积为![]() ,
,
由题意可知,几何体![]() 为直四棱柱,且高为
为直四棱柱,且高为![]() ,
,
因此,几何体![]() 的体积为
的体积为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
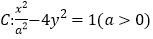 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于 ,抛物线
,抛物线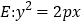 的焦点与双曲线
的焦点与双曲线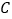 的右焦点重合,则抛物线
的右焦点重合,则抛物线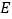 上的动点
上的动点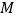 到直线
到直线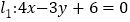 和
和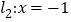 距离之和的最小值为( )
距离之和的最小值为( )A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
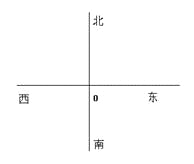
(I)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(II)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体
 中,
中, 、
、 分别为
分别为 、
、 的中点,
的中点, ,
, ,如图.
,如图.
(1)若
 交平面
交平面 于点
于点 ,证明:
,证明: 、
、 、
、 三点共线;
三点共线;(2)线段
 上是否存在点
上是否存在点 ,使得平面
,使得平面 平面
平面 ,若存在确定
,若存在确定 的位置,若不存在说明理由.
的位置,若不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)为二次函数,且
 .
.(1)求f(x)的表达式;
(2)判断函数
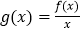 在(0,+∞)上的单调性,并证明.
在(0,+∞)上的单调性,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区上年度电价为
 元/(
元/(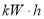 ),年用电量为
),年用电量为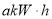 .本年度该地政府实行惠民政策,要求电力部门让利给用户,将电价下调到
.本年度该地政府实行惠民政策,要求电力部门让利给用户,将电价下调到 元/(
元/(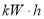 )至
)至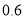 元/(
元/(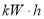 )之间,而用户的期望电价为
)之间,而用户的期望电价为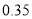 元/(
元/(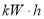 ).经测算,下调电价后新增用电量和实际电价与用户的期望电价的差成反比(比例系数为
).经测算,下调电价后新增用电量和实际电价与用户的期望电价的差成反比(比例系数为 ).该地区的电力成本价为
).该地区的电力成本价为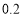 元/(
元/(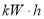 ).
).(1)写出本年度电价下调后电力部门的收益
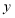 (单位:元)关于实际电价
(单位:元)关于实际电价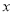 (单位:元/(
(单位:元/(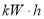 )的函数解析式;(收益
)的函数解析式;(收益 实际用电量
实际用电量 (实际电价
(实际电价 成本价))
成本价))(2)设
 ,当电价最低定为多少时,可保证电力部门的收益比上年至多减少
,当电价最低定为多少时,可保证电力部门的收益比上年至多减少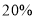 ?
? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如下四个命题:①在线性回归模型中,相关指数
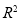 表示解释变量
表示解释变量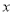 对于预报变量
对于预报变量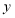 的贡献率,
的贡献率,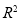 越接近于
越接近于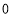 ,表示回归效果越好;②在回归直线方程
,表示回归效果越好;②在回归直线方程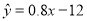 中,当解释变量
中,当解释变量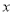 每增加一个单位时,预报变量
每增加一个单位时,预报变量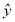 平均增加
平均增加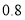 个单位;③两个变量相关性越强,则相关系数的绝对值就越接近于
个单位;③两个变量相关性越强,则相关系数的绝对值就越接近于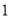 ;④对分类变量
;④对分类变量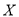 与
与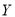 ,对它们的随机变量
,对它们的随机变量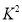 的观测值
的观测值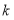 来说,
来说,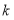 越小,则“
越小,则“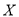 与
与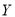 有关系”的把握程度越大.其中正确命题的序号是__________.
有关系”的把握程度越大.其中正确命题的序号是__________.
相关试题

