【题目】某地区上年度电价为![]() 元/(
元/(![]() ),年用电量为
),年用电量为![]() .本年度该地政府实行惠民政策,要求电力部门让利给用户,将电价下调到
.本年度该地政府实行惠民政策,要求电力部门让利给用户,将电价下调到![]() 元/(
元/(![]() )至
)至![]() 元/(
元/(![]() )之间,而用户的期望电价为
)之间,而用户的期望电价为![]() 元/(
元/(![]() ).经测算,下调电价后新增用电量和实际电价与用户的期望电价的差成反比(比例系数为
).经测算,下调电价后新增用电量和实际电价与用户的期望电价的差成反比(比例系数为![]() ).该地区的电力成本价为
).该地区的电力成本价为![]() 元/(
元/(![]() ).
).
(1)写出本年度电价下调后电力部门的收益![]() (单位:元)关于实际电价
(单位:元)关于实际电价![]() (单位:元/(
(单位:元/(![]() )的函数解析式;(收益
)的函数解析式;(收益![]() 实际用电量
实际用电量![]() (实际电价
(实际电价![]() 成本价))
成本价))
(2)设![]() ,当电价最低定为多少时,可保证电力部门的收益比上年至多减少
,当电价最低定为多少时,可保证电力部门的收益比上年至多减少![]() ?
?
参考答案:
【答案】(1)![]() ,
,![]() ;(2)当电价最低定为
;(2)当电价最低定为![]() 元/(
元/(![]() )时,可保证电力部门的收益比上年至多减少
)时,可保证电力部门的收益比上年至多减少![]() .
.
【解析】
(1)设下调电价后新增用电量为![]() ,可得出
,可得出![]() ,进而求出本年度的用电量,再结合收益的计算方法可得出收益
,进而求出本年度的用电量,再结合收益的计算方法可得出收益![]() 关于实际电价
关于实际电价![]() 的函数解析式;
的函数解析式;
(2)根据题意得出 ,解此不等式组,即可得出结论.
,解此不等式组,即可得出结论.
(1)设下调电价后新增用电量为![]() ,
,
因为下调电价后新增用电量和实际电价与用户期望电价的差成反比(比例系数为![]() ),
),
则![]() ,所以本年度的用电量为
,所以本年度的用电量为![]() ,
,
所以本年度电力部门的收益![]() 关于实际电价
关于实际电价![]() 的函数解析式为:
的函数解析式为:![]() ,
,![]() ;
;
(2)依题意有: ,
,
整理得: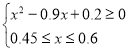 ,解得:
,解得:![]() ,
,
所以当电价最低定为![]() 元/(
元/(![]() )时,可保证电力部门的收益比上年至多减少
)时,可保证电力部门的收益比上年至多减少![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体
 中,
中, 、
、 分别为
分别为 、
、 的中点,
的中点, ,
, ,如图.
,如图.
(1)若
 交平面
交平面 于点
于点 ,证明:
,证明: 、
、 、
、 三点共线;
三点共线;(2)线段
 上是否存在点
上是否存在点 ,使得平面
,使得平面 平面
平面 ,若存在确定
,若存在确定 的位置,若不存在说明理由.
的位置,若不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直四棱柱
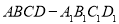 的底面是直角梯形,
的底面是直角梯形,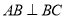 ,
,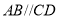 ,
,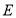 、
、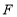 分别是棱
分别是棱 、
、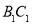 上的动点,且
上的动点,且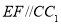 ,
,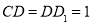 ,
, ,
,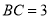 .
.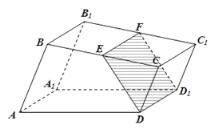
(1)证明:无论点
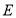 怎样运动,四边形
怎样运动,四边形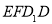 都为矩形;
都为矩形;(2)当
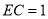 时,求几何体
时,求几何体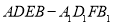 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)为二次函数,且
 .
.(1)求f(x)的表达式;
(2)判断函数
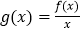 在(0,+∞)上的单调性,并证明.
在(0,+∞)上的单调性,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如下四个命题:①在线性回归模型中,相关指数
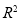 表示解释变量
表示解释变量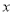 对于预报变量
对于预报变量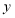 的贡献率,
的贡献率,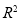 越接近于
越接近于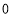 ,表示回归效果越好;②在回归直线方程
,表示回归效果越好;②在回归直线方程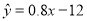 中,当解释变量
中,当解释变量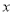 每增加一个单位时,预报变量
每增加一个单位时,预报变量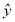 平均增加
平均增加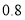 个单位;③两个变量相关性越强,则相关系数的绝对值就越接近于
个单位;③两个变量相关性越强,则相关系数的绝对值就越接近于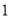 ;④对分类变量
;④对分类变量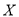 与
与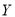 ,对它们的随机变量
,对它们的随机变量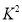 的观测值
的观测值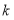 来说,
来说,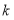 越小,则“
越小,则“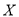 与
与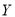 有关系”的把握程度越大.其中正确命题的序号是__________.
有关系”的把握程度越大.其中正确命题的序号是__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】某厂家拟在2020年举行促销活动,经调查测算,某产品的年销售量(即该厂的年产量)
 万件与年促销费用
万件与年促销费用 万元,满足
万元,满足 (
( 为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).
为常数),如果不搞促销活动,则该产品的年销售量只能是1万件,已知2020年生产该产品的固定投入为8万元,每生产1万件,该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金).(1)将2020年该产品的利润
 (万元)表示为年促销费用
(万元)表示为年促销费用 (万元)的函数;
(万元)的函数;(2)该厂家2020年的促销费用投入多少万元时,厂家的利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县共有90间农村淘宝服务站,随机抽取5间,统计元旦期间的网购金额(单位:万元)的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值;
(2)若网购金额(单位:万元)不小于18的服务站定义为优秀服务站,其余为非优秀服务站.根据茎叶图推断90间服务站中有几间优秀服务站?
(3)从随机抽取的5间服务站中再任取2间作网购商品的调查,求恰有1间是优秀服务站的概率.

相关试题

