【题目】已知双曲线![]() 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于![]() ,抛物线
,抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,则抛物线
的右焦点重合,则抛物线![]() 上的动点
上的动点![]() 到直线
到直线![]() 和
和![]() 距离之和的最小值为( )
距离之和的最小值为( )
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】B
【解析】分析:由双曲线的右顶点到渐近线的距离求出![]() ,从而可确定双曲线的方程和焦点坐标,进而得到抛物线的方程和焦点,然后根据抛物线的定义将点M到直线
,从而可确定双曲线的方程和焦点坐标,进而得到抛物线的方程和焦点,然后根据抛物线的定义将点M到直线![]() 的距离转化为到焦点的距离,最后结合图形根据“垂线段最短”求解.
的距离转化为到焦点的距离,最后结合图形根据“垂线段最短”求解.
详解:由双曲线方程![]() 可得,
可得,
双曲线的右顶点为![]() ,渐近线方程为
,渐近线方程为![]() ,即
,即![]() .
.
∵双曲线的右顶点到渐近线的距离等于![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴双曲线的方程为![]() ,
,
∴双曲线的焦点为![]() .
.
又抛物线![]() 的焦点与双曲线
的焦点与双曲线![]() 的右焦点重合,
的右焦点重合,
∴![]() ,
,
∴抛物线的方程为![]() ,焦点坐标为
,焦点坐标为![]() .如图,
.如图,

设点M到直线![]() 的距离为
的距离为![]() ,到直线
,到直线![]() 的距离为
的距离为![]() ,则
,则![]() ,
,
∴![]() .
.
结合图形可得当![]() 三点共线时,
三点共线时,![]() 最小,且最小值为点F到直线
最小,且最小值为点F到直线![]() 的距离
的距离![]() .
.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,长度为3的线段
 的端点
的端点 、
、 分别在
分别在 ,
, 轴上滑动,点
轴上滑动,点 在线段
在线段 上,且
上,且 ,
,(1)若点
 的轨迹为曲线
的轨迹为曲线 ,求其方程;
,求其方程;(2)过点
 的直线
的直线 与曲线
与曲线 交于不同两点
交于不同两点 、
、 ,
, 是曲线上不同于
是曲线上不同于 、
、 的动点,求
的动点,求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知半径为
 的圆的圆心在
的圆的圆心在 轴上,圆心的横坐标是整数,且与直线
轴上,圆心的横坐标是整数,且与直线 相切.
相切.(Ⅰ)求圆的方程;
(Ⅱ)设直线

 与圆相交于
与圆相交于 两点,求实数
两点,求实数 的取值范围;
的取值范围;(Ⅲ) 在(Ⅱ)的条件下,是否存在实数
 ,使得弦
,使得弦 的垂直平分线
的垂直平分线 过点
过点 ,若存在,求出实数
,若存在,求出实数 的值;若不存在,请说明理由
的值;若不存在,请说明理由 -
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某高中学校为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐,规定:每场知识竞赛前三名的得分都分别为
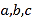
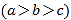 且
且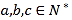 ;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为
;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为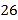 分,乙和丙最后得分都是
分,乙和丙最后得分都是 分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )A. 乙有四场比赛获得第三名
B. 每场比赛第一名得分
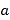 为
为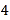
C. 甲可能有一场比赛获得第二名
D. 丙可能有一场比赛获得第一名
-
科目: 来源: 题型:
查看答案和解析>>【题目】某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
(I)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(II)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体
 中,
中, 、
、 分别为
分别为 、
、 的中点,
的中点, ,
, ,如图.
,如图.
(1)若
 交平面
交平面 于点
于点 ,证明:
,证明: 、
、 、
、 三点共线;
三点共线;(2)线段
 上是否存在点
上是否存在点 ,使得平面
,使得平面 平面
平面 ,若存在确定
,若存在确定 的位置,若不存在说明理由.
的位置,若不存在说明理由. -
科目: 来源: 题型:
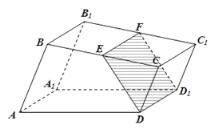
查看答案和解析>>【题目】如图,已知直四棱柱
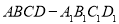 的底面是直角梯形,
的底面是直角梯形,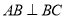 ,
,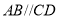 ,
,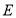 、
、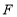 分别是棱
分别是棱 、
、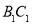 上的动点,且
上的动点,且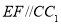 ,
,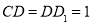 ,
, ,
,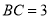 .
.
(1)证明:无论点
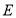 怎样运动,四边形
怎样运动,四边形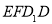 都为矩形;
都为矩形;(2)当
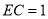 时,求几何体
时,求几何体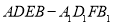 的体积.
的体积.
相关试题

