【题目】在正方体![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,![]() ,如图.
,如图.

(1)若![]() 交平面
交平面![]() 于点
于点![]() ,证明:
,证明:![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 平面
平面![]() ,若存在确定
,若存在确定![]() 的位置,若不存在说明理由.
的位置,若不存在说明理由.
参考答案:
【答案】(1)证明见解析;(2)存在,且![]() .
.
【解析】
(1)先得出![]() 为平面
为平面![]() 与平面
与平面![]() 的交线,然后说明点
的交线,然后说明点![]() 是平面
是平面![]() 与平面
与平面![]() 的公共点,即可得出
的公共点,即可得出![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)设![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,然后证明出平面
,然后证明出平面![]() 平面
平面![]() ,再确定出点
,再确定出点![]() 在
在![]() 上的位置即可.
上的位置即可.
(1)![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以,点
,所以,点![]() 是平面
是平面![]() 和平面
和平面![]() 的一个公共点,同理可知,点
的一个公共点,同理可知,点![]() 也是平面
也是平面![]() 和平面
和平面![]() 的公共点,则平面
的公共点,则平面![]() 和平面
和平面![]() 的交线为
的交线为![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以,点
,所以,点![]() 也是平面
也是平面![]() 和平面
和平面![]() 的公共点,由公理三可知,
的公共点,由公理三可知,![]() ,因此,
,因此,![]() 、
、![]() 、
、![]() 三点共线;
三点共线;
(2)如下图所示:

设![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
下面证明平面![]() 平面
平面![]() .
.
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() ,
,![]() 、
、![]() 平面
平面![]() ,因此,平面
,因此,平面![]() 平面
平面![]() .
.
下面来确定点![]() 的位置:
的位置:
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,所以,
的中点,所以,![]() ,且
,且![]() ,则点
,则点![]() 为
为![]() 的中点,
的中点,
易知![]() ,即
,即![]() ,又
,又![]() ,所以,四边形
,所以,四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() 四边形
四边形![]() 为正方形,且
为正方形,且![]() ,则
,则![]() 为
为![]() 的中点,所以,点
的中点,所以,点![]() 为
为![]() 的中点,
的中点,![]() ,
,
因此,线段![]() 上是否存在点
上是否存在点![]() ,且
,且![]() 时,平面
时,平面![]() 平面
平面![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代儒家要求学生掌握六种基本才艺:礼、乐、射、御、书、数,简称“六艺”,某高中学校为弘扬“六艺”的传统文化,分别进行了主题为“礼、乐、射、御、书、数”六场传统文化知识竞赛,现有甲、乙、丙三位选手进入了前三名的最后角逐,规定:每场知识竞赛前三名的得分都分别为
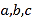
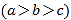 且
且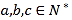 ;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为
;选手最后得分为各场得分之和,在六场比赛后,已知甲最后得分为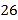 分,乙和丙最后得分都是
分,乙和丙最后得分都是 分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )
分,且乙在其中一场比赛中获得第一名,下列说法正确的是( )A. 乙有四场比赛获得第三名
B. 每场比赛第一名得分
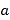 为
为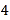
C. 甲可能有一场比赛获得第二名
D. 丙可能有一场比赛获得第一名
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
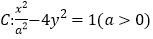 的右顶点到其一条渐近线的距离等于
的右顶点到其一条渐近线的距离等于 ,抛物线
,抛物线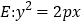 的焦点与双曲线
的焦点与双曲线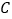 的右焦点重合,则抛物线
的右焦点重合,则抛物线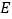 上的动点
上的动点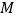 到直线
到直线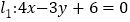 和
和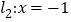 距离之和的最小值为( )
距离之和的最小值为( )A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某港口O要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的O北偏西30°且与该港口相距20海里的A处,并正以30海里/小时的航行速度沿正东方向匀速行驶.假设该小艇沿直线方向以v海里/小时的航行速度匀速行驶,经过t小时与轮船相遇.
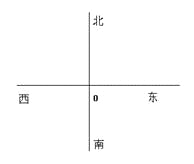
(I)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(II)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直四棱柱
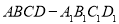 的底面是直角梯形,
的底面是直角梯形,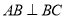 ,
,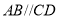 ,
,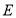 、
、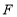 分别是棱
分别是棱 、
、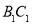 上的动点,且
上的动点,且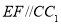 ,
,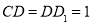 ,
, ,
,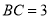 .
.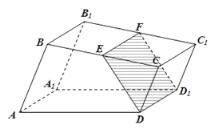
(1)证明:无论点
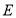 怎样运动,四边形
怎样运动,四边形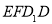 都为矩形;
都为矩形;(2)当
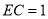 时,求几何体
时,求几何体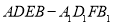 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)为二次函数,且
 .
.(1)求f(x)的表达式;
(2)判断函数
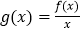 在(0,+∞)上的单调性,并证明.
在(0,+∞)上的单调性,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地区上年度电价为
 元/(
元/(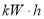 ),年用电量为
),年用电量为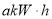 .本年度该地政府实行惠民政策,要求电力部门让利给用户,将电价下调到
.本年度该地政府实行惠民政策,要求电力部门让利给用户,将电价下调到 元/(
元/(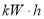 )至
)至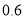 元/(
元/(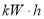 )之间,而用户的期望电价为
)之间,而用户的期望电价为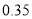 元/(
元/(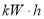 ).经测算,下调电价后新增用电量和实际电价与用户的期望电价的差成反比(比例系数为
).经测算,下调电价后新增用电量和实际电价与用户的期望电价的差成反比(比例系数为 ).该地区的电力成本价为
).该地区的电力成本价为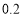 元/(
元/(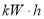 ).
).(1)写出本年度电价下调后电力部门的收益
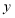 (单位:元)关于实际电价
(单位:元)关于实际电价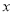 (单位:元/(
(单位:元/(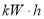 )的函数解析式;(收益
)的函数解析式;(收益 实际用电量
实际用电量 (实际电价
(实际电价 成本价))
成本价))(2)设
 ,当电价最低定为多少时,可保证电力部门的收益比上年至多减少
,当电价最低定为多少时,可保证电力部门的收益比上年至多减少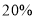 ?
?
相关试题

