【题目】已知:以点![]() (
(![]() )为圆心的圆与
)为圆心的圆与![]() 轴交
轴交
于点O, A,与y轴交于点O, B,其中O为原点.
(1)求证:△OAB的面积为定值;
(2)设直线![]() 与圆C交于点M, N,若OM = ON,求圆C的方程.
与圆C交于点M, N,若OM = ON,求圆C的方程.
参考答案:
【答案】(1)根据条件写成圆的方程,求出点A,B的坐标,进而写出△OAB的面积即可得证;
(2)![]()
【解析】试题分析:(1)设出圆C的方程,求得A、B的坐标,再根据S△AOB=![]() OAOB,计算可得结论.
OAOB,计算可得结论.
(2)设MN的中点为H,则CH⊥MN,根据C、H、O三点共线,KMN=﹣2,由直线OC的斜率![]() ,求得t的值,可得所求的圆C的方程.
,求得t的值,可得所求的圆C的方程.
试题解析:
(1)![]() ,
,![]() .
.
设圆![]() 的方程是
的方程是 ![]()
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]()
![]() ,即:
,即:![]() 的面积为定值.
的面积为定值.
(2)![]()
![]() 垂直平分线段
垂直平分线段![]() .
.
![]() ,
,![]() 直线
直线![]() 的方程是
的方程是![]() .
.
![]() ,解得:
,解得:![]()
当![]() 时,圆心
时,圆心![]() 的坐标为
的坐标为![]() ,
,![]() ,此时
,此时![]() 到直线
到直线![]() 的距离
的距离![]() ,圆
,圆![]() 与直线
与直线![]() 相交于两点.
相交于两点.
当![]() 时,圆心
时,圆心![]() 的坐标为
的坐标为![]() ,
,![]() ,此时
,此时![]() 到直线
到直线![]() 的距离
的距离![]() 圆
圆![]() 与直线
与直线![]() 不相交,
不相交,![]() 不符合题意舍去.
不符合题意舍去.
![]() 圆
圆![]() 的方程为
的方程为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
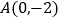 ,椭圆
,椭圆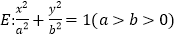 的离心率为
的离心率为 ,
,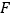 是椭圆
是椭圆 的右焦点,直线
的右焦点,直线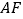 的斜率为
的斜率为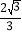 ,
,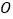 为坐标原点.
为坐标原点.(1)求
 的方程;
的方程;(2)设过点
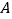 的动直线
的动直线 与
与 相交于
相交于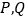 两点,问:是否存在直线
两点,问:是否存在直线 ,使以
,使以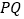 为直径的圆经过原点
为直径的圆经过原点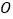 ,若存在,求出对应直线
,若存在,求出对应直线 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2cos2ωx+2sinωxcosωx(ω>0)的最小正周期为π.
(Ⅰ)求f(
 )的值;
)的值;(Ⅱ)求函数f(x)的单调递增区间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x2+y2-2(m+3)x+2(1-4m2)y+16m4+9=0表示一个圆.
(1) 求实数m的取值范围;
(2) 求该圆半径r的取值范围;
(3) 求该圆心的纵坐标的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,五面体
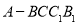 中,
中,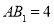 ,底面
,底面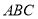 是正三角形,
是正三角形,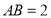 ,四边形
,四边形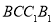 是矩形,二面角
是矩形,二面角 为直二面角.
为直二面角.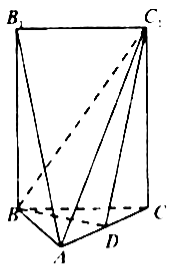
(1)
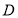 在
在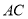 上运动,当
上运动,当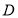 在何处时,有
在何处时,有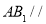 平面
平面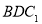 ,并说明理由;
,并说明理由;(2)当
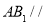 平面
平面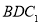 时,求二面角
时,求二面角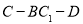 余弦值.
余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
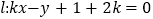 (
(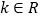 ).
).(1)证明:直线
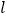 过定点;
过定点;(2)若直线不经过第四象限,求
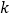 的取值范围;
的取值范围;(3)若直线
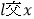 轴负半轴于
轴负半轴于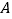 ,交
,交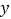 轴正半轴于
轴正半轴于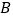 ,△
,△ 的面积为
的面积为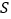 (
(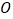 为坐标原点),求
为坐标原点),求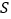 的最小值,并求此时直线
的最小值,并求此时直线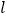 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家之一,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准
 (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过 的部分按平价收费,超出
的部分按平价收费,超出 的部分按议价收费,为了了解居民用水情况,通过抽祥,获得了某年
的部分按议价收费,为了了解居民用水情况,通过抽祥,获得了某年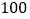 位居民毎人的月均用水量(单位:吨),将数据按照
位居民毎人的月均用水量(单位:吨),将数据按照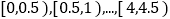 分成
分成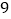 组,制成了如图所示的频率分布直方图.
组,制成了如图所示的频率分布直方图.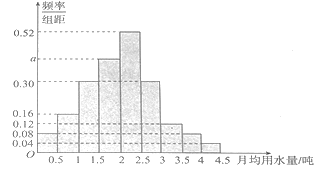
(1)求直方图中
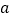 的值;
的值;(2)若该市有
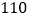 万居民,估计全市居民中月均用水量不低于
万居民,估计全市居民中月均用水量不低于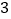 吨的人数,并说明理由;
吨的人数,并说明理由;(3)若该市政府希望使
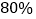 的居民每月的用水量不超过标准
的居民每月的用水量不超过标准 (吨),估计
(吨),估计 的值(精确到
的值(精确到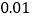 ),并说明理由.
),并说明理由.
相关试题

