【题目】在ABC中,角A,B,C的对边分别为a,b,c,若△ABC为锐角三角形,且满足sinB(1+2cosC)=2sinAcosC+cosAsinC,则下列等式成立的是( )
A.a=2b
B.b=2a
C.A=2B
D.B=2A
参考答案:
【答案】A
【解析】解:在ABC中,角A,B,C的对边分别为a,b,c,满足sinB(1+2cosC)=2sinAcosC+cosAsinC=sinAcosC+sin(A+C)=sinAcosC+sinB,
可得:2sinBcosC=sinAcosC,因为△ABC为锐角三角形,所以2sinB=sinA,
由正弦定理可得:2b=a.
故选:A.
【考点精析】本题主要考查了两角和与差的正弦公式和正弦定理的定义的相关知识点,需要掌握两角和与差的正弦公式:![]() ;正弦定理:
;正弦定理:![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设{an}和{bn}是两个等差数列,记cn=max{b1﹣a1n,b2﹣a2n,…,bn﹣ann}(n=1,2,3,…),其中max{x1 , x2 , …,xs}表示x1 , x2 , …,xs这s个数中最大的数.(13分)
(1)若an=n,bn=2n﹣1,求c1 , c2 , c3的值,并证明{cn}是等差数列;
(2)证明:或者对任意正数M,存在正整数m,当n≥m时, >M;或者存在正整数m,使得cm , cm+1 , cm+2 , …是等差数列.
>M;或者存在正整数m,使得cm , cm+1 , cm+2 , …是等差数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代数学名著《九章算术》中“竹九节”问题曰:“今有竹九节,下三节容量四升,上四节容量三升,问中间两节欲均容各多少?”其意为:“现有一根9节的竹子,自上而下的容积成等差数列,下面3节容量为4升,上面4节容积为3升,问中间2节各多少容积?”则中间2节容积合计________升
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于给定的正整数k,若数列{an}满足:an﹣k+an﹣k+1+…+an﹣1+an+1+…an+k﹣1+an+k=2kan对任意正整数n(n>k)总成立,则称数列{an}是“P(k)数列”.
(Ⅰ)证明:等差数列{an}是“P(3)数列”;
(Ⅱ)若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列
 的公差
的公差 ,数列
,数列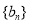 满足
满足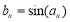 ,集合
,集合 .
.(1)若
 ,
, ,求集合
,求集合 ;
;(2)若
 ,求
,求 使得集合
使得集合 恰有两个元素;
恰有两个元素;(3)若集合
 恰有三个元素,
恰有三个元素, ,T是不超过5的正整数,求T的所有可能值,并写出与之相应的一个等差数列
,T是不超过5的正整数,求T的所有可能值,并写出与之相应的一个等差数列 的通项公式及集合
的通项公式及集合 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某届奥运会上,中国队以26金18银26铜的成绩称金牌榜第三、奖牌榜第二,某校体育爱好者在高三年级一班至六班进行了“本届奥运会中国队表现”的满意度调查
 结果只有“满意”和“不满意”两种
结果只有“满意”和“不满意”两种 ,从被调查的学生中随机抽取了50人,具体的调查结果如表:
,从被调查的学生中随机抽取了50人,具体的调查结果如表:班号
一班
二班
三班
四班
五班
六班
频数
5
9
11
9
7
9
满意人数
4
7
8
5
6
6
(1)在高三年级全体学生中随机抽取一名学生,由以上统计数据估计该生持满意态度的概率;
(2)若从一班至二班的调查对象中随机选取4人进行追踪调查,记选中的4人中对“本届奥运会中国队表现”不满意的人数为
 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1:y=cosx,C2:y=sin(2x+
 ),则下面结论正确的是( )
),则下面结论正确的是( )
A.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B.把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C.把C1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移  个单位长度,得到曲线C2
个单位长度,得到曲线C2
D.把C1上各点的横坐标缩短到原来的 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移  个单位长度,得到曲线C2
个单位长度,得到曲线C2
相关试题

