【题目】设函数f(x)= ![]() ,其中k<﹣2.
,其中k<﹣2.
(1)求函数f(x)的定义域D(用区间表示);
(2)讨论函数f(x)在D上的单调性;
(3)若k<﹣6,求D上满足条件f(x)>f(1)的x的集合(用区间表示).
参考答案:
【答案】
(1)解:设t=x2+2x+k,则f(x)等价为y=g(t)= ![]() ,
,
要使函数有意义,则t2+2t﹣3>0,解得t>1或t<﹣3,
即x2+2x+k>1或x2+2x+k<﹣3,
则(x+1)2>2﹣k,①或(x+1)2<﹣2﹣k,②,
∵k<﹣2,∴2﹣k>﹣2﹣k,
由①解得x+1> ![]() 或x+1
或x+1 ![]() ,即x>
,即x> ![]() ﹣1或x
﹣1或x ![]() ,
,
由②解得﹣ ![]() <x+1<
<x+1< ![]() ,即﹣1﹣
,即﹣1﹣ ![]() <x<﹣1+
<x<﹣1+ ![]() ,
,
综上函数的定义域为( ![]() ﹣1,+∞)∪(﹣∞,﹣1﹣
﹣1,+∞)∪(﹣∞,﹣1﹣ ![]() )∪(﹣1﹣
)∪(﹣1﹣ ![]() ,﹣1+
,﹣1+ ![]() )
)
(2)解:f′(x)= ![]() =
= ![]()
=﹣ ![]() ,
,
由f'(x)>0,即2(x2+2x+k+1)(x+1)<0,则(x+1+ ![]() )(x+1﹣
)(x+1﹣ ![]() )(x+1)<0
)(x+1)<0
解得x<﹣1﹣ ![]() 或﹣1<x<﹣1+
或﹣1<x<﹣1+ ![]() ,结合定义域知,x<﹣1﹣
,结合定义域知,x<﹣1﹣ ![]() 或﹣1<x<﹣1+
或﹣1<x<﹣1+ ![]() ,
,
即函数的单调递增区间为:(﹣∞,﹣1﹣ ![]() ),(﹣1,﹣1+
),(﹣1,﹣1+ ![]() ),
),
同理解得单调递减区间为:(﹣1﹣ ![]() ,﹣1),(﹣1+
,﹣1),(﹣1+ ![]() ,+∞)
,+∞)
(3)解:由f(x)=f(1)得(x2+2x+k)2+2(x2+2x+k)﹣3=(3+k)2+2(3+k)﹣3,
则[(x2+2x+k)2﹣(3+k)2]+2[(x2+2x+k)﹣(3+k)]=0,
∴(x2+2x+2k+5)(x2+2x﹣3)=0
即(x+1+ ![]() )(x+1﹣
)(x+1﹣ ![]() )(x+3)(x﹣1)=0,
)(x+3)(x﹣1)=0,
∴x=﹣1﹣ ![]() 或x=﹣1+
或x=﹣1+ ![]() 或x=﹣3或x=1,
或x=﹣3或x=1,
∵k<﹣6,
∴1∈(﹣1,﹣1+ ![]() ),﹣3∈(﹣1﹣
),﹣3∈(﹣1﹣ ![]() ,﹣1),
,﹣1),
∵f(﹣3)=f(1)=f(﹣1﹣ ![]() )=f(﹣1+
)=f(﹣1+ ![]() ),
),
且满足﹣1﹣ ![]() ∈(﹣∞,﹣1﹣
∈(﹣∞,﹣1﹣ ![]() ),﹣1+
),﹣1+ ![]() ∈(﹣1+
∈(﹣1+ ![]() ,+∞),
,+∞),
由(2)可知函数f(x)在上述四个区间内均单调递增或递减,结合图象,要使f(x)>
f(1)的集合为:
( ![]() )∪(﹣1﹣
)∪(﹣1﹣ ![]() ,﹣3)∪(1,﹣1+
,﹣3)∪(1,﹣1+ ![]() )∪(﹣1+
)∪(﹣1+ ![]() ,﹣1+
,﹣1+ ![]() )
)
【解析】(1)利用换元法,结合函数成立的条件,即可求出函数的定义域.(2)根据复合函数的定义域之间的关系即可得到结论.(3)根据函数的单调性,即可得到不等式的解集.
【考点精析】本题主要考查了函数的定义域及其求法和函数单调性的性质的相关知识点,需要掌握求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集才能正确解答此题.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零;函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
 +
+  =1(a>b>0)的右焦点为(
=1(a>b>0)的右焦点为(  ,0),离心率为
,0),离心率为  .
.
(1)求椭圆C的标准方程;
(2)若动点P(x0 , y0)为椭圆C外一点,且点P到椭圆C的两条切线相互垂直,求点P的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式
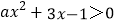 的解集是,
的解集是,
(1)求a的值;
(2)求不等式
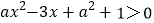 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
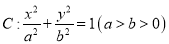 的一个焦点为
的一个焦点为 ,离心率为
,离心率为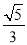 .
.(1)求椭圆
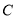 的标准方程;
的标准方程;(2)若动点
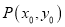 为椭圆外一点,且点
为椭圆外一点,且点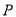 到椭圆
到椭圆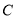 的两条切线相互垂直,求点
的两条切线相互垂直,求点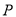 的轨迹方程.
的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某学校准备修建一个面积为2400平方米的矩形活动场地(图中ABCD)的围栏,按照修建要求,中间用围墙EF隔开,使得ABEF为矩形,EFCD为正方形,设
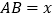 米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.
米,已知围墙(包括EF)的修建费用均为每米500元,设围墙(包括EF)的修建总费用为y元.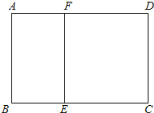
(1)求出y关于x的函数解析式及x的取值范围;
(2)当x为何值时,围墙(包括EF)的修建总费用y最小?并求出y的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于茎叶图的说法,结论错误的一个是( )

A. 甲的极差是29 B. 甲的中位数是25
C. 乙的众数是21 D. 甲的平均数比乙的大
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是 ( )
A. 某事件发生的概率为1.1 B. 对立事件也是互斥事件
C. 不能同时发生的的两个事件是两个对立事件 D. 某事件发生的概率是随着实验次数的变化而变化的
相关试题

