【题目】已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的右焦点为(
=1(a>b>0)的右焦点为( ![]() ,0),离心率为
,0),离心率为 ![]() .
.
(1)求椭圆C的标准方程;
(2)若动点P(x0 , y0)为椭圆C外一点,且点P到椭圆C的两条切线相互垂直,求点P的轨迹方程.
参考答案:
【答案】
(1)解:依题意知 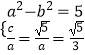 ,求得a=3,b=2,
,求得a=3,b=2,
∴椭圆的方程为 ![]() +
+ ![]() =1
=1
(2)解:①当两条切线中有一条斜率不存在时,即A、B两点分别位于椭圆长轴与短轴的端点,P的坐标为(±3,±2),符合题意,
②当两条切线斜率均存在时,设过点P(x0,y0)的切线为y=k(x﹣x0)+y0,
![]() +
+ ![]() =
= ![]() +
+ ![]() =1,整理得(9k2+4)x2+18k(y0﹣kx0)x+9[(y0﹣kx0)2﹣4]=0,
=1,整理得(9k2+4)x2+18k(y0﹣kx0)x+9[(y0﹣kx0)2﹣4]=0,
∴△=[18k(y0﹣kx0)]2﹣4(9k2+4)×9[(y0﹣kx0)2﹣4]=0,
整理得(x02﹣9)k2﹣2x0×y0×k+(y02﹣4)=0,
∴﹣1=k1k2= ![]() =﹣1,
=﹣1,
∴x02+y02=13.
把点(±3,±2)代入亦成立,
∴点P的轨迹方程为:x2+y2=13
【解析】(1)根据焦点坐标和离心率求得a和b,则椭圆的方可得.(2)设出切线的方程,带入椭圆方程,整理后利用△=0,整理出关于k的一元二次方程,利用韦达定理表示出k1k2 , 进而取得x0和y0的关系式,即P点的轨迹方程.
【考点精析】利用椭圆的标准方程对题目进行判断即可得到答案,需要熟知椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为正方形.PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
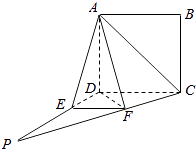
(1)证明:CF⊥平面ADF;
(2)求二面角D﹣AF﹣E的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设数列{an}的前n项和为Sn , 满足Sn=2nan+1﹣3n2﹣4n,n∈N* , 且S3=15.
(1)求a1 , a2 , a3的值;
(2)求数列{an}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知双曲线
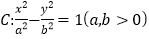 的离心率为
的离心率为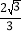 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.(1)求双曲线C的方程;
(2)直线y=kx+m(k≠0, m≠0)与该双曲线C交于不同的两点C,D,且C,D两点都在以点A为圆心的同一圆上,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式
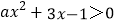 的解集是,
的解集是,
(1)求a的值;
(2)求不等式
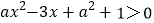 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
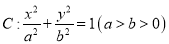 的一个焦点为
的一个焦点为 ,离心率为
,离心率为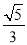 .
.(1)求椭圆
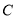 的标准方程;
的标准方程;(2)若动点
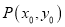 为椭圆外一点,且点
为椭圆外一点,且点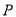 到椭圆
到椭圆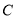 的两条切线相互垂直,求点
的两条切线相互垂直,求点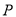 的轨迹方程.
的轨迹方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=
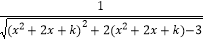 ,其中k<﹣2.
,其中k<﹣2.
(1)求函数f(x)的定义域D(用区间表示);
(2)讨论函数f(x)在D上的单调性;
(3)若k<﹣6,求D上满足条件f(x)>f(1)的x的集合(用区间表示).
相关试题

