【题目】已知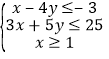 ,(本题不作图不得分)
,(本题不作图不得分)
(1)求![]() 的最大值和最小值;
的最大值和最小值;
(2)求![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)最大值为12,最小值3; (2)![]() .
.
【解析】
(1)由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,把最优解的坐标代入目标函数得结论;(2)![]() 的几何意义表示区域内的点与
的几何意义表示区域内的点与![]() 连接直线的斜率,可得与
连接直线的斜率,可得与![]() 连接的直线斜率最小,与
连接的直线斜率最小,与![]() 连接的直线斜率最大,从而可得结果.
连接的直线斜率最大,从而可得结果.
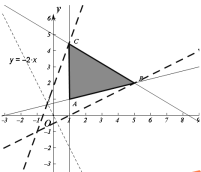
(1)由已知得到平面区域:z=2x+y变形为y=-2x+z,
当此直线经过图中A时使得直线在y轴的截距最小,z最小,
经过图中B时在y轴的截距最大,z 最大,A(1,1),B(5,2),
所以z=2x+y的最大值为2×5+2=12,最小值2×1+1=3;
(2)![]() 的几何意义表示区域内的点与(-1,-1)连接直线的斜率,
的几何意义表示区域内的点与(-1,-1)连接直线的斜率,
所以与B连接的直线斜率最小,与C连接的直线斜率最大,
所以![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]()
所以![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列有关命题的说法正确的是( )
A.命题“若xy=0,则x=0”的否命题为:“若xy=0,则x≠0”
B.“若x+y=0,则x,y互为相反数”的逆命题为真命题
C.命题“x∈R,使得2x2﹣1<0”的否定是:“x∈R,均有2x2﹣1<0”
D.命题“若cosx=cosy,则x=y”的逆否命题为真命题 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A.函数y=f(x)?g(x)的周期为2
B.函数y=f(x)?g(x)的最大值为1
C.将f(x)的图象向左平移 个单位后得到g(x)的图象
个单位后得到g(x)的图象
D.将f(x)的图象向右平移 个单位后得到g(x)的图象
个单位后得到g(x)的图象 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图四边形ABCD为菱形,G为AC与BD交点,
 ,
,(I)证明:平面
 平面
平面 ;
;(II)若
 ,
, 三棱锥
三棱锥 的体积为
的体积为 ,求该三棱锥的侧面积.
,求该三棱锥的侧面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数f(x)=
 ,称为狄利克雷函数,则关于函数f(x)有以下四个命题: ①f(f(x))=1;
,称为狄利克雷函数,则关于函数f(x)有以下四个命题: ①f(f(x))=1;
②函数f(x)是偶函数;
③任意一个非零有理数T,f(x+T)=f(x)对任意x∈R恒成立;
④存在三个点A(x1 , f(x1)),B(x2 , f(x2)),C(x3 , f(x3)),使得△ABC为等边三角形.
其中真命题的个数是( )
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
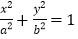 (a>b>0)的两个焦点分别为F1,F2,离心率为
(a>b>0)的两个焦点分别为F1,F2,离心率为 ,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.(1)求椭圆C的方程;
(2)若直线y=kx+b与椭圆C分别交于A,B两点,且OA⊥OB,试问点O到直线AB的距离是否为定值,证明你的结论.
相关试题

