【题目】德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数f(x)= ![]() ,称为狄利克雷函数,则关于函数f(x)有以下四个命题: ①f(f(x))=1;
,称为狄利克雷函数,则关于函数f(x)有以下四个命题: ①f(f(x))=1;
②函数f(x)是偶函数;
③任意一个非零有理数T,f(x+T)=f(x)对任意x∈R恒成立;
④存在三个点A(x1 , f(x1)),B(x2 , f(x2)),C(x3 , f(x3)),使得△ABC为等边三角形.
其中真命题的个数是( )
A.4
B.3
C.2
D.1
参考答案:
【答案】A
【解析】解:①∵当x为有理数时,f(x)=1;当x为无理数时,f(x)=0, ∴当x为有理数时,ff((x))=f(1)=1;当x为无理数时,f(f(x))=f(0)=1,
即不管x是有理数还是无理数,均有f(f(x))=1,故①正确;
②∵有理数的相反数还是有理数,无理数的相反数还是无理数,
∴对任意x∈R,都有f(﹣x)=f(x),故②正确;
③若x是有理数,则x+T也是有理数; 若x是无理数,则x+T也是无理数,
∴根据函数的表达式,任取一个不为零的有理数T,f(x+T)=f(x)对x∈R恒成立,故③正确;
④取x1=﹣ ![]() ,x2=0,x3=
,x2=0,x3= ![]() ,可得f(x1)=0,f(x2)=1,f(x3)=0,
,可得f(x1)=0,f(x2)=1,f(x3)=0,
∴A( ![]() ,0),B(0,1),C(﹣
,0),B(0,1),C(﹣ ![]() ,0),恰好△ABC为等边三角形,故④正确.
,0),恰好△ABC为等边三角形,故④正确.
即真命题的个数是4个,
故选:A.
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M,
(1)求过点M且到点P(0,4)的距离为2的直线l的方程;
(2)求过点M且与直线l3:x+3y+1=0平行的直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
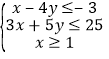 ,(本题不作图不得分)
,(本题不作图不得分)(1)求
 的最大值和最小值;
的最大值和最小值; (2)求
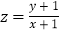 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图四边形ABCD为菱形,G为AC与BD交点,
 ,
,(I)证明:平面
 平面
平面 ;
;(II)若
 ,
, 三棱锥
三棱锥 的体积为
的体积为 ,求该三棱锥的侧面积.
,求该三棱锥的侧面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
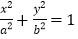 (a>b>0)的两个焦点分别为F1,F2,离心率为
(a>b>0)的两个焦点分别为F1,F2,离心率为 ,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.
,过F1的直线l与椭圆C交于M,N两点,且△MNF2的周长为8.(1)求椭圆C的方程;
(2)若直线y=kx+b与椭圆C分别交于A,B两点,且OA⊥OB,试问点O到直线AB的距离是否为定值,证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足
 ,则使不等式a2016>2017成立的所有正整数a1的集合为( )
,则使不等式a2016>2017成立的所有正整数a1的集合为( )
A.{a1|a1≥2017,a1∈N+}
B.{a1|a1≥2016,a1∈N+}
C.{a1|a1≥2015,a1∈N+}
D.{a1|a1≥2014,a1∈N+} -
科目: 来源: 题型:
查看答案和解析>>【题目】雾霾大气严重影响人们的生活,某科技公司拟投资开发新型节能环保产品,策划部制定投资计划时,不仅要考虑可能获得的盈利,而且还要考虑可能出现的亏损,经过市场调查,公司打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为
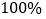 和
和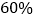 ,可能的最大亏损率分别为
,可能的最大亏损率分别为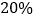 和
和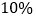 ,投资人计划投资金额不超过9万元,要求确保可能的资金亏损不超过
,投资人计划投资金额不超过9万元,要求确保可能的资金亏损不超过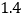 万元.
万元. Ⅰ
Ⅰ 若投资人用x万元投资甲项目,y万元投资乙项目,试写出x,y所满足的条件,并在直角坐标系内作出表示x,y范围的图形.
若投资人用x万元投资甲项目,y万元投资乙项目,试写出x,y所满足的条件,并在直角坐标系内作出表示x,y范围的图形. Ⅱ
Ⅱ 根据
根据 的规划,投资公司对甲、乙两个项目分别投资多少万元,才能使可能的盈利最大?
的规划,投资公司对甲、乙两个项目分别投资多少万元,才能使可能的盈利最大?
相关试题

