【题目】国内,某知名连接店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖的有效展开,参与抽奖活动的人数越来越多,该分店经理对开业前7天参加抽奖活动的人数进行统计, ![]() 表示开业第
表示开业第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:

经过进一步的统计分析,发现![]() 与
与![]() 具有线性相关关系.
具有线性相关关系.
(1)如从这7天中随便机抽取两天,求至少有1天参加抽奖人数超过10天的概率;
(2)根据上表给出的数据,用最小二乘法,求出![]() 与
与![]() 的线性回归方程
的线性回归方程![]() ,并估计若该活动持续10天,共有多少名顾客参加抽奖.
,并估计若该活动持续10天,共有多少名顾客参加抽奖.
参考公式: 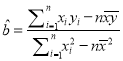 ,
, ![]() ,
, ![]() ,
, ![]() .
.
参考答案:
【答案】(1)![]() (2)140
(2)140
【解析】试题分析:(1)先利用枚举法确定7天中随便机抽取两天总事件数,从中确定至少有1天参加抽奖人数超过10的事件数,最后根据古典概型概率公式求概率,(2)先求平均数![]() ,代入公式
,代入公式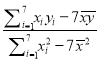 求
求![]() ,利用
,利用![]() 求
求![]() ,即得线性回归方程,再利用线性回归方程估计
,即得线性回归方程,再利用线性回归方程估计![]() 时参加抽奖的人数,得到此次抽奖活动总人数.
时参加抽奖的人数,得到此次抽奖活动总人数.
试题解析:(Ⅰ)这7天中参加抽奖的人数没有超过10的为第1,2,3,4天,超过10的为第5,6,7天,从这7天中任取两天的情况有![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,共21种,其中至少有1天参加抽奖人数超过10的有15种,所以
,共21种,其中至少有1天参加抽奖人数超过10的有15种,所以![]() .
.
(Ⅱ)依题意: ![]() .
.
![]() ,
, ![]() ,
, ![]() ,
,
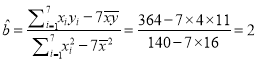 ,
, ![]() ,
,
则![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,
,
预测![]() 时
时![]() ,
, ![]() 时,
时, ![]() ,
, ![]() 时
时![]() ,
,
则此次活动参加抽奖的人数约为![]() 人.
人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某颜料公司生产
 两种产品,其中生产每吨
两种产品,其中生产每吨 产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨
产品,需要甲染料1吨,乙染料4吨,丙染料2吨,生产每吨 产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果
产品,需要甲染料1吨,乙染料0吨,丙染料5吨,且该公司一条之内甲、乙、丙三种染料的用量分别不超过50吨,160吨和200吨,如果 产品的利润为300元/吨,
产品的利润为300元/吨,  产品的利润为200元/吨,则该颜料公司一天之内可获得最大利润为( )
产品的利润为200元/吨,则该颜料公司一天之内可获得最大利润为( )A. 14000元 B. 16000元 C. 18000元 D. 20000元
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
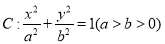 的左、右焦点分别为
的左、右焦点分别为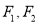 ,点
,点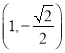 是椭圆
是椭圆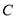 上的点,离心率为
上的点,离心率为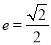 .
.(1)求椭圆
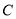 的方程;
的方程;(2)点
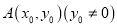 在椭圆上
在椭圆上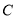 上,若点
上,若点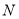 与点
与点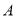 关于原点的对称,连接
关于原点的对称,连接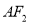 ,并延长与椭圆
,并延长与椭圆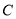 的另一个交点为
的另一个交点为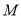 ,连接
,连接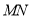 ,求
,求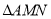 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某造船公司年造船量是20艘,已知造船x艘的产值函数为R(x)=3 700x+45x2-10x3(单位:万元),成本函数为C(x)=460x-5 000(单位:万元).
(1)求利润函数P(x);(提示:利润=产值-成本)
(2)问年造船量安排多少艘时,可使公司造船的年利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
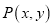 满足条件
满足条件 .
.(Ⅰ)求点
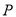 的轨迹
的轨迹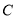 的方程;
的方程;(Ⅱ)直线
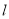 与圆
与圆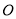 :
: 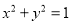 相切,与曲线
相切,与曲线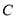 相较于
相较于 ,
, 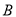 两点,若
两点,若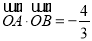 ,求直线
,求直线 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足an+1=
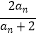 ,a1=1,n∈N* .
,a1=1,n∈N* .
(1)求a2 , a3 , a4的值;
(2)求数列{an}的通项公式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图所示的三棱柱
 中,棱
中,棱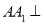 底面
底面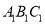 ,
, 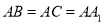 ,
, 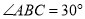 ,
, 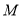 ,
, 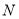 ,
, 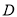 分别是
分别是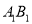 ,
, 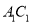 ,
, 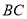 的中点.
的中点.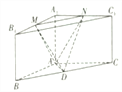
(Ⅰ)求证:
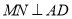 ;
;(Ⅱ)求为二面角
 的余弦值.
的余弦值.
相关试题

