【题目】已知数列{an}满足an+1= ![]() ,a1=1,n∈N* .
,a1=1,n∈N* .
(1)求a2 , a3 , a4的值;
(2)求数列{an}的通项公式.
参考答案:
【答案】
(1)解:∵数列{an}满足an+1= ![]() ,a1=1,n∈N*.∴a2=
,a1=1,n∈N*.∴a2= ![]() =
= ![]() ,同理可得:a3=
,同理可得:a3= ![]() ,a4=
,a4= ![]() .
.
(2)解:数列{an}满足an+1= ![]() ,a1=1,n∈N*.
,a1=1,n∈N*.
两边取倒数可得: ![]() =
= ![]() +
+ ![]() ,即
,即 ![]() ﹣
﹣ ![]() =
= ![]() ,
,
∴数列 ![]() 是等差数列,首项为1,公差为
是等差数列,首项为1,公差为 ![]() ,
,
∴ ![]() =1+
=1+ ![]() (n﹣1),解得an=
(n﹣1),解得an= ![]() ,
,
∴an= ![]()
【解析】(1)由数列{an}满足an+1= ![]() ,a1=1,n∈N* . 分别令n=1,2,3,即可得出.(2)数列{an}满足an+1=
,a1=1,n∈N* . 分别令n=1,2,3,即可得出.(2)数列{an}满足an+1= ![]() ,a1=1,n∈N* . 两边取倒数可得:
,a1=1,n∈N* . 两边取倒数可得: ![]() ﹣
﹣ ![]() =
= ![]() ,再利用等差数列的通项公式即可得出.
,再利用等差数列的通项公式即可得出.
【考点精析】利用数列的通项公式对题目进行判断即可得到答案,需要熟知如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某造船公司年造船量是20艘,已知造船x艘的产值函数为R(x)=3 700x+45x2-10x3(单位:万元),成本函数为C(x)=460x-5 000(单位:万元).
(1)求利润函数P(x);(提示:利润=产值-成本)
(2)问年造船量安排多少艘时,可使公司造船的年利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】国内,某知名连接店分店开张营业期间,在固定的时间段内消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖的有效展开,参与抽奖活动的人数越来越多,该分店经理对开业前7天参加抽奖活动的人数进行统计,
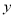 表示开业第
表示开业第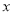 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
经过进一步的统计分析,发现
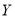 与
与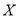 具有线性相关关系.
具有线性相关关系.(1)如从这7天中随便机抽取两天,求至少有1天参加抽奖人数超过10天的概率;
(2)根据上表给出的数据,用最小二乘法,求出
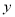 与
与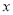 的线性回归方程
的线性回归方程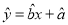 ,并估计若该活动持续10天,共有多少名顾客参加抽奖.
,并估计若该活动持续10天,共有多少名顾客参加抽奖.参考公式:
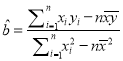 ,
, 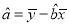 ,
, 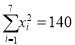 ,
,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
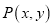 满足条件
满足条件 .
.(Ⅰ)求点
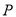 的轨迹
的轨迹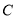 的方程;
的方程;(Ⅱ)直线
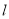 与圆
与圆 :
: 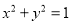 相切,与曲线
相切,与曲线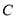 相较于
相较于 ,
, 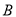 两点,若
两点,若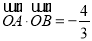 ,求直线
,求直线 的斜率.
的斜率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如下图所示的三棱柱
 中,棱
中,棱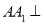 底面
底面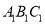 ,
, 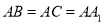 ,
, 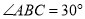 ,
,  ,
, 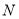 ,
, 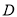 分别是
分别是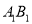 ,
, 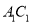 ,
, 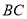 的中点.
的中点.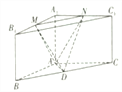
(Ⅰ)求证:
 ;
;(Ⅱ)求为二面角
 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( )
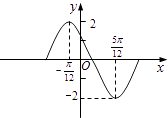
A.y=2sin(2x+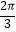 )
)
B.y=2sin(2x+ )
)
C.y=2sin( ﹣
﹣  )
)
D.y=2sin(2x﹣ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知非零向量
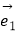 ,
, 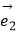 ,
,  ,
, 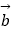 满足
满足  =2
=2 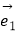 ﹣
﹣ 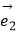 ,
, 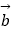 =k
=k 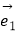 +
+ 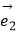 ,给出以下结论:
,给出以下结论:
①若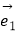 与
与 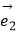 不共线,
不共线,  与
与 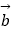 共线,则k=﹣2;
共线,则k=﹣2;
②若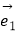 与
与 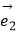 不共线,
不共线,  与
与 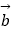 共线,则k=2;
共线,则k=2;
③存在实数k,使得 与
与 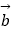 不共线,
不共线, 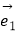 与
与 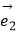 共线;
共线;
④不存在实数k,使得 与
与 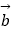 不共线,
不共线, 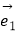 与
与 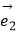 共线.
共线.
其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
相关试题

