【题目】已知直线![]() 及点
及点![]() .
.
(1)证明直线![]() 过某定点,并求该定点的坐标;
过某定点,并求该定点的坐标;
(2)当点![]() 到直线
到直线![]() 的距离最大时,求直线
的距离最大时,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1)证明见解析,定点坐标为![]() ;(2)15x+24y+2=0.
;(2)15x+24y+2=0.
【解析】试题分析:(1)直线l的方程可化为 a(2x+y+1)+b(-x+y-1)=0,由![]() ,即可解得定点;
,即可解得定点;
(2)由(1)知直线l恒过定点A![]() ,当直线l垂直于直线PA时,点P到直线l的距离最大,利用点斜式求直线方程即可.
,当直线l垂直于直线PA时,点P到直线l的距离最大,利用点斜式求直线方程即可.
试题解析:
(1)证明:直线l的方程可化为 a(2x+y+1)+b(-x+y-1)=0,
由![]() ,
,
得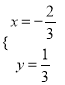 ,所以直线l恒过定点
,所以直线l恒过定点![]() .
.
(2)由(1)知直线l恒过定点A![]() ,
,
当直线l垂直于直线PA时,点P到直线l的距离最大.
又直线PA的斜率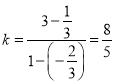 ,所以直线l的斜率kl=-
,所以直线l的斜率kl=-![]() .
.
故直线l的方程为![]() ,
,
即15x+24y+2=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
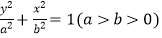 的两顶点为A,B如图,离心率为
的两顶点为A,B如图,离心率为 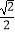 ,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.
,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.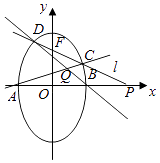
(Ⅰ)当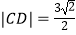 时,求直线l的方程;
时,求直线l的方程;
(Ⅱ)当点P异于A,B两点时,求证: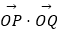 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,设二次函数
中,设二次函数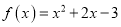 的图像与两坐标轴有三个交点,经过这三点的圆记为
的图像与两坐标轴有三个交点,经过这三点的圆记为
(1)求圆
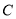 的方程;
的方程; (2)若过点
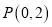 的直线
的直线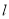 与圆
与圆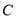 相交,所截得的弦长为4,求直线
相交,所截得的弦长为4,求直线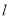 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣1,1,2)、B(1,0,﹣1),设D在直线AB上,且
 =2
=2  ,设C(λ,
,设C(λ,  +λ,1+λ),若CD⊥AB,则λ的值为( )
+λ,1+λ),若CD⊥AB,则λ的值为( )
A.
B.﹣
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在棱长为4的正方体ABCD﹣A1B1C1D1中,点E是棱CC1的中点,则异面直线D1E与AC所成角的余弦值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是定义在
是定义在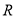 上的奇函数,当
上的奇函数,当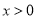 时,
时, 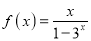 .
.(1)求
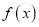 的解析式;
的解析式;(2)解不等式
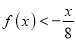 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
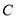 经过点
经过点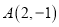 ,
,  和直线
和直线 相切.
相切.(1)求圆
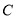 的方程;
的方程;(2)若直线
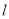 经过点
经过点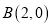 ,并且被圆
,并且被圆 截得的弦长为2,求直线
截得的弦长为2,求直线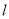 的方程.
的方程.
相关试题

