【题目】在平面直角坐标系![]() 中,设二次函数
中,设二次函数![]() 的图像与两坐标轴有三个交点,经过这三点的圆记为
的图像与两坐标轴有三个交点,经过这三点的圆记为![]()
(1)求圆![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交,所截得的弦长为4,求直线
相交,所截得的弦长为4,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() 或
或![]() .
.
【解析】试题分析:(1)先求得圆的三个交点,,由![]() 和
和![]() 的垂直平分线得圆心,进而得半径;
的垂直平分线得圆心,进而得半径;
(2)易得圆心到直线的距离为1,讨论直线斜率不存在和存在时,利用圆心到直线的距离求解即可.
试题解析:
二次函数![]() 的图像与两坐标轴轴的三个交点分别记为
的图像与两坐标轴轴的三个交点分别记为![]()
(1)线段![]() 的垂直平分线为
的垂直平分线为![]() ,线段
,线段![]() 的垂直平分线
的垂直平分线![]() ,
,
两条中垂线的交点为圆心![]() ,又半径
,又半径![]() ,
,
∴圆的方程为: ![]()
(2)已知圆的半径![]() ,弦长为4,所以圆心到直线的距离为1,
,弦长为4,所以圆心到直线的距离为1,
若直线斜率不存在时,即![]() 时,满足题意;
时,满足题意;
当直线斜率存在时,设直线斜率存在为![]() ,直线方程为
,直线方程为![]()
![]() ,此时直线方程为:
,此时直线方程为: ![]() ,
,
所以直线![]() 的方程为:
的方程为: ![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
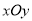 中,圆
中,圆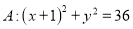 ,点
,点 ,点
,点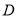 是圆
是圆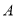 上的动点,线段
上的动点,线段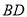 的垂直平分线交线段
的垂直平分线交线段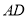 于点
于点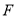 ,设
,设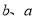 分别为点
分别为点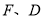 的横坐标,定义函数
的横坐标,定义函数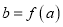 ,给出下列结论:
,给出下列结论:①
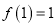 ;②
;②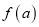 是偶函数;③
是偶函数;③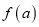 在定义域上是增函数;
在定义域上是增函数;④
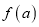 图象的两个端点关于圆心
图象的两个端点关于圆心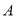 对称;
对称;⑤动点
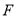 到两定点
到两定点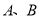 的距离和是定值.
的距离和是定值.其中正确的是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,
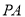 是圆柱的母线,
是圆柱的母线, 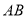 是圆柱底面圆的直径,
是圆柱底面圆的直径, 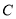 是底面圆周上异于
是底面圆周上异于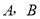 的任意一点,
的任意一点, 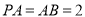 .
.(1)求证:
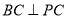 ;
;(2)求三棱锥
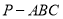 体积的最大值,并写出此时三棱锥
体积的最大值,并写出此时三棱锥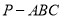 外接球的表面积.
外接球的表面积.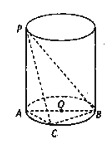
-
科目: 来源: 题型:
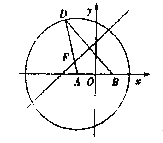
查看答案和解析>>【题目】椭圆
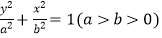 的两顶点为A,B如图,离心率为
的两顶点为A,B如图,离心率为 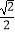 ,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.
,过其焦点F(0,1)的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.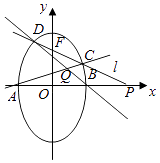
(Ⅰ)当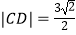 时,求直线l的方程;
时,求直线l的方程;
(Ⅱ)当点P异于A,B两点时,求证: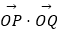 为定值.
为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣1,1,2)、B(1,0,﹣1),设D在直线AB上,且
 =2
=2  ,设C(λ,
,设C(λ,  +λ,1+λ),若CD⊥AB,则λ的值为( )
+λ,1+λ),若CD⊥AB,则λ的值为( )
A.
B.﹣
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 及点
及点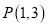 .
.(1)证明直线
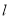 过某定点,并求该定点的坐标;
过某定点,并求该定点的坐标;(2)当点
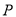 到直线
到直线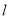 的距离最大时,求直线
的距离最大时,求直线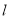 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在棱长为4的正方体ABCD﹣A1B1C1D1中,点E是棱CC1的中点,则异面直线D1E与AC所成角的余弦值是 .

相关试题

