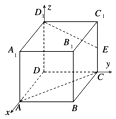
【题目】如图所示,在棱长为4的正方体ABCD﹣A1B1C1D1中,点E是棱CC1的中点,则异面直线D1E与AC所成角的余弦值是 . 
参考答案:
【答案】![]()
【解析】解:如图,建立空间直角坐标系,
则A(4,0,0),C(0,4,0),D1(0,0,4),E(0,4,2),
![]() =(﹣4,4,0),
=(﹣4,4,0), ![]() =(0,4,﹣2).
=(0,4,﹣2).
cos< ![]() ,
, ![]() >=
>= 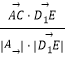 =
= ![]() =
= ![]() .
.
∴异面直线D1E与AC所成角的余弦值为 ![]() .
.
所以答案是: ![]() .
.
【考点精析】根据题目的已知条件,利用异面直线及其所成的角的相关知识可以得到问题的答案,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
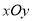 中,设二次函数
中,设二次函数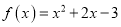 的图像与两坐标轴有三个交点,经过这三点的圆记为
的图像与两坐标轴有三个交点,经过这三点的圆记为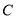
(1)求圆
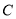 的方程;
的方程; (2)若过点
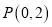 的直线
的直线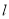 与圆
与圆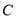 相交,所截得的弦长为4,求直线
相交,所截得的弦长为4,求直线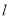 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣1,1,2)、B(1,0,﹣1),设D在直线AB上,且
 =2
=2  ,设C(λ,
,设C(λ,  +λ,1+λ),若CD⊥AB,则λ的值为( )
+λ,1+λ),若CD⊥AB,则λ的值为( )
A.
B.﹣
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 及点
及点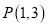 .
.(1)证明直线
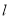 过某定点,并求该定点的坐标;
过某定点,并求该定点的坐标;(2)当点
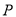 到直线
到直线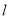 的距离最大时,求直线
的距离最大时,求直线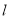 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是定义在
是定义在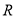 上的奇函数,当
上的奇函数,当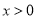 时,
时, 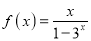 .
.(1)求
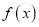 的解析式;
的解析式;(2)解不等式
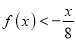 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
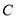 经过点
经过点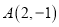 ,
,  和直线
和直线 相切.
相切.(1)求圆
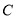 的方程;
的方程;(2)若直线
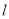 经过点
经过点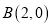 ,并且被圆
,并且被圆 截得的弦长为2,求直线
截得的弦长为2,求直线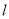 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四面体
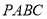 中,
中, 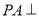 平面
平面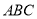 ,
, 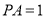 ,
, 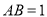 ,
,  ,
,  .
.(Ⅰ)求四面体
 的四个面的面积中,最大的面积是多少?
的四个面的面积中,最大的面积是多少?(Ⅱ)证明:在线段
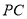 上存在点
上存在点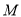 ,使得
,使得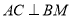 ,并求
,并求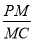 的值.
的值.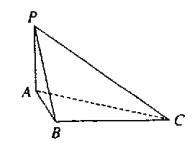
相关试题

