【题目】已知圆![]() 经过点
经过点![]() ,
, ![]() 和直线
和直线![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)若直线![]() 经过点
经过点![]() ,并且被圆
,并且被圆![]() 截得的弦长为2,求直线
截得的弦长为2,求直线![]() 的方程.
的方程.
参考答案:
【答案】(1)(x-1)2+(y+2)2=2;(2)x=2或3x-4y-6=0.
【解析】试题分析:(1)先求线段AB的垂直平分线方程为![]() ,设圆心的坐标为C(a,-a-1),由圆心到点的距离和到切线的距离相等求解即可;
,设圆心的坐标为C(a,-a-1),由圆心到点的距离和到切线的距离相等求解即可;
(2)由题知圆心C到直线l的距离![]() ,进而讨论直线斜率存在不存在两种情况求解即可.
,进而讨论直线斜率存在不存在两种情况求解即可.
试题解析:
(1)由题知,线段AB的中点M(1,-2), ![]() ,
,
线段AB的垂直平分线方程为![]() ,即
,即![]() ,
,
设圆心的坐标为C(a,-a-1),
则![]() ,
,
化简,得a2-2a+1=0,解得a=1.∴C(1,-2),
半径r=|AC|=![]() =
=![]() .
.
∴圆C的方程为(x-1)2+(y+2)2=2.
(解二:可设原方程用待定系数法求解)
(2)由题知圆心C到直线l的距离![]() ,
,
①当直线l的斜率不存在时,直线l的方程为x=2,此时直线l被圆C截得的弦长为2,
满足条件.
②当直线l的斜率存在时,设直线l的方程为![]() ,由题意得
,由题意得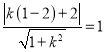 ,
,
解得k=![]() ,
,
∴直线l的方程为y=![]() (x-2).
(x-2).
综上所述,直线l的方程为x=2或3x-4y-6=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 及点
及点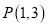 .
.(1)证明直线
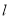 过某定点,并求该定点的坐标;
过某定点,并求该定点的坐标;(2)当点
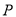 到直线
到直线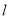 的距离最大时,求直线
的距离最大时,求直线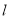 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在棱长为4的正方体ABCD﹣A1B1C1D1中,点E是棱CC1的中点,则异面直线D1E与AC所成角的余弦值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 是定义在
是定义在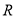 上的奇函数,当
上的奇函数,当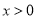 时,
时, 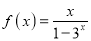 .
.(1)求
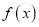 的解析式;
的解析式;(2)解不等式
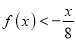 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四面体
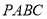 中,
中, 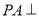 平面
平面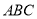 ,
, 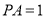 ,
, 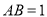 ,
,  ,
,  .
.(Ⅰ)求四面体
 的四个面的面积中,最大的面积是多少?
的四个面的面积中,最大的面积是多少?(Ⅱ)证明:在线段
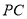 上存在点
上存在点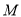 ,使得
,使得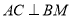 ,并求
,并求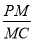 的值.
的值.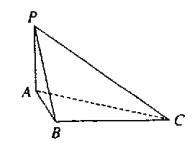
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
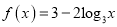 ,
, 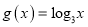 .
.(1)当
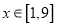 时,求函数
时,求函数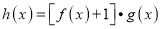 的值域;
的值域;(2)如果对任意的
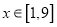 ,不等式
,不等式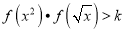 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;(3)是否存在实数
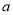 ,使得函数
,使得函数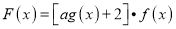 的最大值为0,若存在,求出
的最大值为0,若存在,求出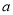 的值,若不存在,说明理由.
的值,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程
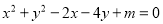 .
.(Ⅰ)若此方程表示圆,求
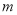 的取值范围;
的取值范围;(Ⅱ)若(Ⅰ)中的圆与直线
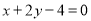 相交于
相交于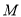 ,
, 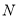 两点,且
两点,且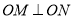 (
(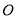 为坐标原点),求
为坐标原点),求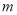 ;
;(Ⅲ)在(Ⅱ)的条件下,求以
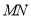 为直径的圆的方程.
为直径的圆的方程.
相关试题

