【题目】已知椭圆C: ![]() 的离心率为
的离心率为 ![]() ,右焦点为F,点B(0,1)在椭圆C上.
,右焦点为F,点B(0,1)在椭圆C上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点 ![]() 的直线交椭圆C于M,N两点,交直线x=2于点P,设
的直线交椭圆C于M,N两点,交直线x=2于点P,设 ![]() ,
, ![]() ,求证:λ+μ为定值.
,求证:λ+μ为定值.
参考答案:
【答案】解:(Ⅰ)由点B(0,1)在椭圆C: ![]() 上,则
上,则 ![]() ,即b=1.
,即b=1.
又椭圆C的离心率为 ![]() ,则
,则 ![]() ,
,
由a2=b2+c2 , 得 ![]() .
.
∴椭圆C的方程为 ![]()
(Ⅱ)证明:由已知得F(1,0),直线MN的斜率存在.
设直线MN的方程为y=k(x﹣1),M(x1 , y1),N(x2 , y2),则P(2,k).
由 ![]() ,
, ![]() ,得
,得 ![]() ,
,
∴ ![]() ,.
,.
联立 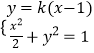 得(1+2k2)x2﹣4k2x+2k2﹣2=0.
得(1+2k2)x2﹣4k2x+2k2﹣2=0.
∴ ![]() ,
, ![]() .
.
∴ ![]() =
= ![]() =0,
=0,
∴λ+μ=0为定值
【解析】(Ⅰ)由题意b=1,利用椭圆的离心率即可求得a的值,求得椭圆方程;(Ⅱ)设直线MN的方程为y=k(x﹣1),代入椭圆方程,利用韦达定理及向量的坐标运算,即可证明λ+μ=0为定值.
【考点精析】本题主要考查了椭圆的标准方程的相关知识点,需要掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 与
与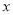 轴负半轴相交于点
轴负半轴相交于点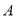 ,与
,与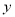 轴正半轴相交于点
轴正半轴相交于点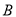 .
.(1)若过点
 的直线
的直线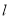 被圆
被圆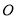 截得的弦长为
截得的弦长为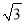 ,求直线
,求直线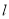 的方程;
的方程;(2)若在以
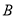 为圆心半径为
为圆心半径为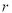 的圆上存在点
的圆上存在点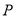 ,使得
,使得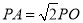 (
(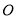 为坐标原点),求
为坐标原点),求 的取值范围;
的取值范围;(3)设
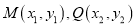 是圆
是圆 上的两个动点,点
上的两个动点,点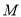 关于原点的对称点为
关于原点的对称点为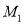 ,点
,点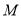 关于
关于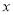 轴的对称点为
轴的对称点为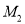 ,如果直线
,如果直线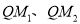 与
与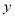 轴分别交于
轴分别交于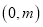 和
和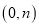 ,问
,问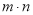 是否为定值?若是求出该定值;若不是,请说明理由.
是否为定值?若是求出该定值;若不是,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校高三年级进行了一次学业水平测试,用系统抽样的方法抽取了50名学生的数学成绩,准备进行分析和研究.经统计,成绩的分组及各组的频数如下:
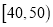 ,2;
,2; 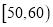 ,3;
,3; 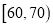 ,10;
,10; 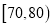
15;
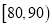 ,12;
,12; 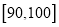 ,8.
,8.(1)完成样本的频率分布表,画出频率分布直方图;
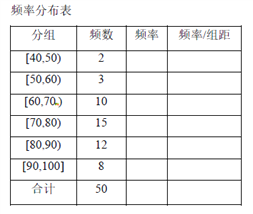
(2)估计成绩在85分以下的学生比例;
(3)请你根据以上信息去估计样本的众数、中位数、平均数(精确到0.01).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
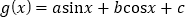 .
.(1)当
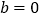 时,求
时,求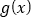 的值域;
的值域;(2)当
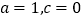 时,函数
时,函数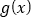 的图象关于
的图象关于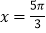 对称,求函数
对称,求函数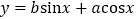 的对称轴.
的对称轴.(3)若
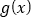 图象上有一个最低点
图象上有一个最低点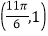 ,如果图象上每点纵坐标不变,横坐标缩短到原来的
,如果图象上每点纵坐标不变,横坐标缩短到原来的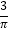 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得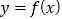 的图象,又知
的图象,又知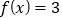 的所有正根从小到大依次为
的所有正根从小到大依次为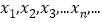 ,且
,且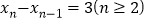 ,求
,求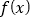 的解析式.
的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】在锐角△ABC中,角A,B,C所对的边分别为a,b,c,已知a=bcosC+
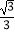 csinB.
csinB.
(1)若a=2,b= ,求c
,求c
(2)设函数y=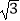 sin(2A﹣30°)﹣2sin2(C﹣15°),求y的取值范围.
sin(2A﹣30°)﹣2sin2(C﹣15°),求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,斜三棱柱ABC﹣A1B1C1的底面是直角三角形,∠ACB=90°,点B1在底面内的射影恰好是BC的中点,且BC=CA=2.

(1)求证:平面ACC1A1⊥平面B1C1CB;
(2)若二面角B﹣AB1﹣C1的余弦值为 ,求斜三棱柱ABC﹣A1B1C1的侧棱AA1的长度.
,求斜三棱柱ABC﹣A1B1C1的侧棱AA1的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
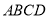 为正方形,
为正方形, 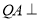 平面
平面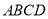 ,
, 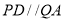 ,
,  .试结合向量法:(1)证明:平面
.试结合向量法:(1)证明:平面 平面
平面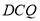 ;
;(2)求二面角
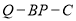 的余弦值.
的余弦值.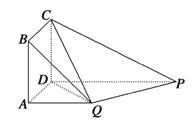
相关试题

