(本小题满分12分)
设二次 函数
函数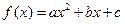 在区间
在区间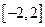 上的最大值、最小值分别是M、m,集合
上的最大值、最小值分别是M、m,集合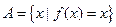 .
.
(1)若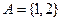 ,且
,且 ,求M和m的值;
,求M和m的值;
(2)若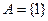 ,且
,且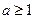 ,记
,记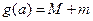 ,求
,求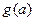 的最小值.
的最小值.
参考答案:
(1)由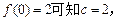 ……………………………1分
……………………………1分
又
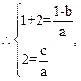 …………………3分
…………………3分 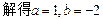 …………4分
…………4分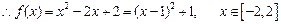
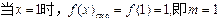 ……………………………5分
……………………………5分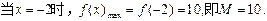 ……………………………6分
……………………………6分
(2)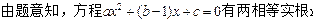 x=1
x=1
∴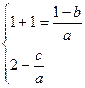 ,即
,即 ……………………………8分
……………………………8分
∴f(x)=ax2+(1-2a)x+a, x∈[-2,2] 其对称轴方程为x=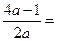

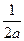
又a≥1,故1- ……………………………9分
……………………………9分
∴M=f(-2)="9a-2 " …………………………10分
m= ……………………………11分
……………………………11分
g(a)=M+m=9a- -1
-1 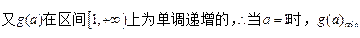 =
= ………12分
………12分
解析
-
科目: 来源: 题型:解答题
查看答案和解析>>(14分)设关于x的函数
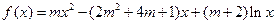 ,其中m为R上的常数,若函数
,其中m为R上的常数,若函数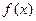 在x=1处取得极大值0,
在x=1处取得极大值0,
(1)求实数m的值;
(2)若函数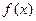 的图像与直线y=k有两个交点,求实数k的取值范围;
的图像与直线y=k有两个交点,求实数k的取值范围;
(3)设函数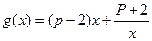 ,若对
,若对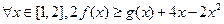 恒成立,
恒成立,
求实数p的取值范围。 -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)化简或求值:
(1)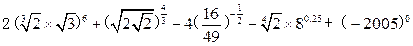
(2)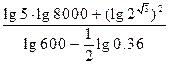 。
。 -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)已知函数
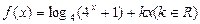 为偶函数.
为偶函数.
(Ⅰ) 求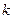 的值;
的值;
(Ⅱ) 若方程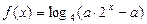 有且只有一个根, 求实数
有且只有一个根, 求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分12分)已知二次函数f(x)=ax2+bx+c.
(1)若f(-1)=0,试判断函数f(x)零点的个数;
(2)是否存在a,b,c∈R,使f(x)同时满足以下条件:
①对任意x∈R,f(-1+x)=f(-1-x),且f(x)≥0;
②对任意x∈R,都有0≤f(x)-x≤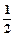 (x-1)2.若存在,求出a,b,c的值;若不存在,请说
(x-1)2.若存在,求出a,b,c的值;若不存在,请说
明理由。
(3)若对任意x1、x2∈R且x1<x2,f(x1)≠f(x2),试证明:存在x0∈(x1,x2),使f(x0)=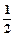 [f(x1)+f(x2)]成立。
[f(x1)+f(x2)]成立。 -
科目: 来源: 题型:解答题
查看答案和解析>>(本小题满分16分)
设 ,
, ,函数
,函数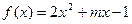
(1)设不等式 的解集为C,当
的解集为C,当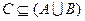 时,求实数
时,求实数 取值范围
取值范围
(2)若对任意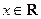 ,都有
,都有 成立,试求
成立,试求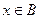 时,
时,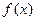 的值
的值 域
域
(3)设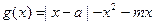
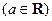 ,求
,求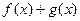 的最小值
的最小值 -
科目: 来源: 题型:解答题
查看答案和解析>>(本题满分13分)
已知函数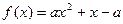 (
(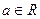 )
)
(1)若函数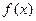 有最大值
有最大值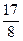 ,求实数a的值; (2)解不等式
,求实数a的值; (2)解不等式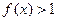 (a∈R).
(a∈R).
相关试题

