【题目】已知圆![]() ,一动圆与直线
,一动圆与直线![]() 相切且与圆
相切且与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若经过定点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点, ![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 作
作![]() 轴的平行线与曲线
轴的平行线与曲线![]() 相交于点
相交于点![]() ,试问是否存在直线
,试问是否存在直线![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
参考答案:
【答案】(1) ![]() ;(2) 存在直线
;(2) 存在直线![]() 或
或![]() ,使得
,使得![]() .
.
【解析】试题分析:
(1)本题用直接法求动点轨迹方程,设支点坐标为![]() ,当然由已知分析,动点不能在
,当然由已知分析,动点不能在![]() 轴左侧,然后利用直线与圆相切和两圆外切的条件列出方程,化简即可;
轴左侧,然后利用直线与圆相切和两圆外切的条件列出方程,化简即可;
(2)假设存在满足题意的直线,设出直线方程,分析发现直线的斜率为0时不合题意,从而设直线方程为![]() ,设
,设![]() ,直线方程与曲线方程联立方程组,消去变量
,直线方程与曲线方程联立方程组,消去变量![]() 后得
后得![]() 的一元二次方程,由韦达定理得
的一元二次方程,由韦达定理得![]() ,设
,设![]() ,得
,得![]() ,
, ![]() ,由
,由![]() 求出
求出![]() 值,得直线方程,若不能求出实数
值,得直线方程,若不能求出实数![]() ,则说明假设错误,不存在相应的直线.
,则说明假设错误,不存在相应的直线.
试题解析:
(1)设![]() ,分析可知:动圆的圆心不能在
,分析可知:动圆的圆心不能在![]() 轴的左侧,故
轴的左侧,故![]() ,
,
∵动圆与直线![]() 相切,且与圆
相切,且与圆![]() 外切,
外切,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
化简可得![]() ;
;
(2)设![]() ,
,
由题意可知,当直线![]() 与
与![]() 轴垂直时,显然不符合题意,
轴垂直时,显然不符合题意,
故可设直线![]() 的方程为
的方程为![]() ,
,
联立![]() 和
和![]() 并消去
并消去![]() ,可得
,可得![]() ,
,
显然![]() ,由韦达定理可知
,由韦达定理可知![]() ,①
,①
又∵![]() ,
,
∴![]() ,②
,②
∵![]() ,∴
,∴![]() ,③
,③
假设存在![]() ,使得
,使得![]() ,
,
由题意可知![]() ,∴
,∴![]() ,④
,④
由![]() 点在抛物线上可知
点在抛物线上可知![]() ,即
,即![]() ,⑤
,⑤
又![]() ,
,
若![]() ,则
,则![]() ,
,
由①②③④⑤代入上式化简可得![]() ,
,
即![]() ,
,
∴![]() ,故
,故![]() ,
,
∴存在直线![]() 或
或![]() ,使得
,使得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC中,a,b,c分别是角A,B,C的对边,且a=80,b=100,A=
 ,则此三角形是( )
,则此三角形是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.锐角或钝角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an},{bn}满足a1=1,且an , an+1是函数f(x)=x2﹣bnx+2n的两个零点,则b10等于( )
A.24
B.32
C.48
D.64 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱
 中,
中, 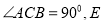 为
为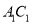 的中点,
的中点,  .
.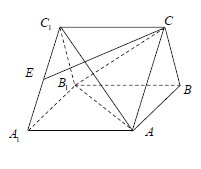
(1)证明:
 平面
平面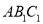 ;
;(2)若
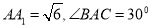 ,求点
,求点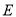 到平面
到平面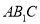 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
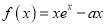 (
(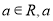 为常数),
为常数), 为自然对数的底数.
为自然对数的底数.(1)当
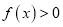 时,求实数
时,求实数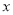 的取值范围;
的取值范围;(2)当
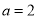 时,求使得
时,求使得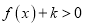 成立的最小正整数
成立的最小正整数 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
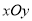 中,圆
中,圆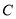 的方程为
的方程为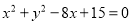 ,若直线
,若直线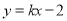 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆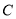 有公共点,则
有公共点,则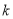 的最大值为__________.
的最大值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内有n(n∈N*)条直线,其中任何两条不平行,任何三条不过同一点,若这n条直线把平面分成f(n)个平面区域,则f(3)=;f(n)= .
相关试题

