【题目】设函数![]() (
(![]() 为常数),
为常数),![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,求实数
时,求实数![]() 的取值范围;
的取值范围;
(2)当![]() 时,求使得
时,求使得![]() 成立的最小正整数
成立的最小正整数![]() .
.
参考答案:
【答案】(1)见解析;(2) 最小正整数![]() 的值为1.
的值为1.
【解析】试题分析:
(1)解不等式![]() ,考虑到
,考虑到![]() 恒成立,可对
恒成立,可对![]() 分类讨论:
分类讨论: ![]() 和
和![]() ;(2)题意就是
;(2)题意就是![]() 恒成立,求
恒成立,求![]() 的最小值正整数,只要求得
的最小值正整数,只要求得![]() 的最小值即可,由于要求得
的最小值即可,由于要求得![]() 的零点,因此还要对此函数进行分析,设
的零点,因此还要对此函数进行分析,设![]() ,利用导数确定它的单调性,从而确定零点
,利用导数确定它的单调性,从而确定零点![]() 的范围,
的范围, ![]() ,再求得最小值
,再求得最小值![]() 的范围,可得结论.
的范围,可得结论.
试题解析:
(1)由![]() 可知
可知![]() ,
,
当![]() 时,
时, ![]() ,由
,由![]() ,解得
,解得![]() ;
;
当![]() 时,
时, ![]() ,由
,由![]() ,解得
,解得![]() 或
或![]() ;
;
当![]() 时,
时, ![]() ,由
,由![]() ,解得
,解得![]() 或
或![]() ;
;
(2)当![]() 时,要使
时,要使![]() 恒成立,即
恒成立,即![]() 恒成立,
恒成立,
令![]() ,则
,则![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,函数
,函数![]() 的
的![]() 上单调递增.
上单调递增.
又因为![]() 时,
时, ![]() ,且
,且![]() ,
,
所以,存在唯一的![]() ,使得
,使得![]() ,
,
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递增.
上单调递增.
所以,当![]() 时,
时, ![]() 取到最小值.
取到最小值.
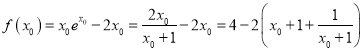 ,
,
因为![]() ,所以
,所以![]() ,
,
从而使得![]() 恒成立的最小正整数
恒成立的最小正整数![]() 的值为1.
的值为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an},{bn}满足a1=1,且an , an+1是函数f(x)=x2﹣bnx+2n的两个零点,则b10等于( )
A.24
B.32
C.48
D.64 -
科目: 来源: 题型:
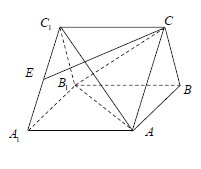
查看答案和解析>>【题目】如图,在直三棱柱
 中,
中, 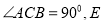 为
为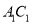 的中点,
的中点,  .
.
(1)证明:
 平面
平面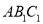 ;
;(2)若
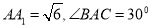 ,求点
,求点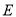 到平面
到平面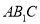 的距离.
的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
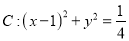 ,一动圆与直线
,一动圆与直线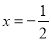 相切且与圆
相切且与圆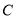 外切.
外切.(1)求动圆圆心
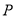 的轨迹
的轨迹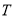 的方程;
的方程;(2)若经过定点
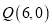 的直线
的直线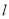 与曲线
与曲线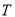 交于
交于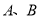 两点,
两点, 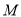 是线段
是线段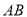 的中点,过
的中点,过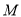 作
作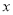 轴的平行线与曲线
轴的平行线与曲线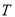 相交于点
相交于点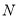 ,试问是否存在直线
,试问是否存在直线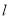 ,使得
,使得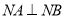 ,若存在,求出直线
,若存在,求出直线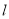 的方程,若不存在,说明理由.
的方程,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
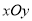 中,圆
中,圆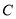 的方程为
的方程为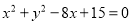 ,若直线
,若直线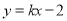 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆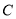 有公共点,则
有公共点,则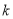 的最大值为__________.
的最大值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面内有n(n∈N*)条直线,其中任何两条不平行,任何三条不过同一点,若这n条直线把平面分成f(n)个平面区域,则f(3)=;f(n)= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角△ABC的面积等于3
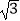 ,且AB=3,AC=4.
,且AB=3,AC=4.
(1)求sin( +A)的值;
+A)的值;
(2)求cos(A﹣B)的值.
相关试题

