【题目】在平面内有n(n∈N*)条直线,其中任何两条不平行,任何三条不过同一点,若这n条直线把平面分成f(n)个平面区域,则f(3)=;f(n)= .
参考答案:
【答案】7;![]()
【解析】解:一条直线(k=1)把平面分成了2部分,记为f(1)=2,f(2)=4,f(3)=7,…
设前k条直线把平面分成了f(k)部分,
第k+1条直线与原有的k条直线有k个交点,这k个交点将第k+1条直线分为k+1段,
这k+1段将平面上原来的f(k)部分的每一部分分成了2个部分,共2(k+1)部分,相当于增加了k+1个部分,
∴第k+1条直线将平面分成了f(k+1)部分,
则f(k+1)﹣f(k)=k+1,令k=1,2,3,….n得
f(2)﹣f(1)=2,f(3)﹣f(2)=3,…,f(n)﹣f(n﹣1)=n,
把这n﹣1个等式累加,得 f(n)=2+ ![]() =2+
=2+ ![]() =
= ![]() .
.
所以答案是:7, ![]() .
.
【考点精析】通过灵活运用归纳推理,掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
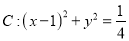 ,一动圆与直线
,一动圆与直线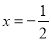 相切且与圆
相切且与圆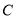 外切.
外切.(1)求动圆圆心
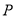 的轨迹
的轨迹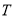 的方程;
的方程;(2)若经过定点
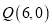 的直线
的直线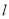 与曲线
与曲线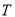 交于
交于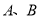 两点,
两点, 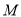 是线段
是线段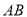 的中点,过
的中点,过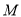 作
作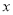 轴的平行线与曲线
轴的平行线与曲线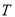 相交于点
相交于点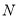 ,试问是否存在直线
,试问是否存在直线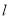 ,使得
,使得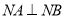 ,若存在,求出直线
,若存在,求出直线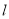 的方程,若不存在,说明理由.
的方程,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
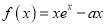 (
(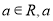 为常数),
为常数), 为自然对数的底数.
为自然对数的底数.(1)当
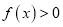 时,求实数
时,求实数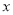 的取值范围;
的取值范围;(2)当
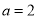 时,求使得
时,求使得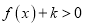 成立的最小正整数
成立的最小正整数 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
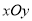 中,圆
中,圆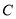 的方程为
的方程为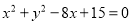 ,若直线
,若直线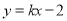 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆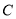 有公共点,则
有公共点,则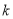 的最大值为__________.
的最大值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角△ABC的面积等于3
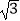 ,且AB=3,AC=4.
,且AB=3,AC=4.
(1)求sin( +A)的值;
+A)的值;
(2)求cos(A﹣B)的值. -
科目: 来源: 题型:
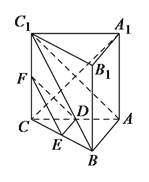
查看答案和解析>>【题目】如图,在三棱柱
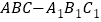 中,
中,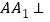 底面
底面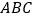 ,
,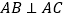
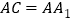 ,
,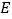 、
、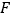 分别是棱
分别是棱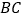 、
、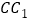 的中点.
的中点.(Ⅰ)求证:
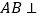 平面
平面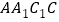 .
.(Ⅱ)若线段
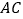 上的点
上的点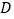 满足平面
满足平面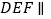 平面
平面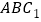 ,试确定点
,试确定点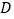 的位置,并说明理由.
的位置,并说明理由.(Ⅲ)证明:
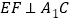 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在“新零售”模式的背景下,某大型零售公司咪推广线下分店,计划在
 市的
市的 区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记
区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记 表示在各区开设分店的个数,
表示在各区开设分店的个数,  表示这个
表示这个 个分店的年收入之和.
个分店的年收入之和. (个)
(个)2
3
4
5
6
 (百万元)
(百万元)2.5
3
4
4.5
6
(1)该公司已经过初步判断,可用线性回归模型拟合
 与
与 的关系,求
的关系,求 关于
关于 的线性回归方程
的线性回归方程 ;
;(2)假设该公司在
 区获得的总年利润
区获得的总年利润 (单位:百万元)与
(单位:百万元)与 之间的关系为
之间的关系为 ,请结合(1)中的线性回归方程,估算该公司应在
,请结合(1)中的线性回归方程,估算该公司应在 区开设多少个分时,才能使
区开设多少个分时,才能使 区平均每个分店的年利润最大?
区平均每个分店的年利润最大?(参考公式:
 ,其中
,其中 )
)
相关试题

