【题目】已知数列{an}的前n项和为Sn , 且an是Sn与2的等差中项,数列{bn}中,b1=1,点P(bn , bn+1)在直线x﹣y+2=0上.
(1)求a1和a2的值;
(2)求数列{an},{bn}的通项an和bn;
(3)设cn=anbn , 求数列{cn}的前n项和Tn .
参考答案:
【答案】
(1)解:∵an是Sn与2的等差中项
∴Sn=2an﹣2∴a1=S1=2a1﹣2,解得a1=2
a1+a2=S2=2a2﹣2,解得a2=4
(2)解:∵Sn=2an﹣2,Sn﹣1=2an﹣1﹣2,
又Sn﹣Sn﹣1=an,n≥2
∴an=2an﹣2an﹣1,
∵an≠0,
∴ ![]() =2(n≥2),即数列{an}是等比数列,∵a1=2,∴an=2n
=2(n≥2),即数列{an}是等比数列,∵a1=2,∴an=2n
∵点P(bn,bn+1)在直线x﹣y+2=0上,∴bn﹣bn+1+2=0,
∴bn+1﹣bn=2,即数列{bn}是等差数列,又b1=1,∴bn=2n﹣1
(3)解:∵cn=(2n﹣1)2n
∴Tn=a1b1+a2b2+…+anbn=1×2+3×22+5×23+…+(2n﹣1)2n,
∴2Tn=1×22+3×23+…+(2n﹣3)2n+(2n﹣1)2n+1
因此:﹣Tn=1×2+(2×22+2×23+…+2×2n)﹣(2n﹣1)2n+1,
即:﹣Tn=1×2+(23+24+…+2n+1)﹣(2n﹣1)2n+1,
∴Tn=(2n﹣3)2n+1+6
【解析】(1)先利用an是Sn与2的等差中项把1代入即可求a1 , 再把2代入即可求a2的值;(2)利用Sn=2an﹣2,可得Sn﹣1=2an﹣1﹣2,两式作差即可求数列{an}的相邻两项之间的关系,找到规律即可求出通项;对于数列{bn},直接利用点P(bn , bn+1)在直线x﹣y+2=0上,代入得数列{bn}是等差数列即可求通项;(3)先把所求结论代入求出数列{cn}的通项,再利用数列求和的错位相减法即可求出其各项的和.
【考点精析】通过灵活运用数列的前n项和,掌握数列{an}的前n项和sn与通项an的关系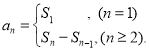 即可以解答此题.
即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

 .
.(Ⅰ)若
 在
在 上单调递减,求
上单调递减,求 的取值范围;
的取值范围;(Ⅱ)讨论
 的单调性.
的单调性. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
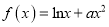 ,
, 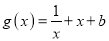 ,且直线
,且直线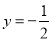 是函数
是函数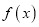 的一条切线.
的一条切线.(Ⅰ)求
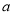 的值;
的值;(Ⅱ)对任意的
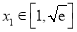 ,都存在
,都存在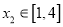 ,使得
,使得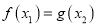 ,求
,求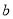 的取值范围;
的取值范围;(Ⅲ)已知方程
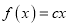 有两个根
有两个根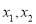 (
(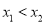 ),若
),若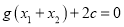 ,求证:
,求证: 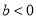 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某单位招聘职工分为笔试和面试两个环节,将笔试成绩合格(满分100分,及格60分,精确到个位数)的应聘者进行统计,得到如下的频率分布表:
分组
频数
频率
[60,70]
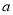
0.16
(70,80]
22
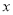
(80,90]
14
0.28
(90,100]
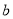

合计
50
1
(Ⅰ)确定表中
 的值(直接写出结果,不必写过程)
的值(直接写出结果,不必写过程)(Ⅱ)面试规定,笔试成绩在80分(不含80分)以上者可以进入面试环节,面试时又要分两关,首先面试官依次提出4个问题供选手回答,并规定,答对2道题就终止回答,通过第一关可以进入下一关,如果前三题均没有答对,则不再回答第四题并且不能进入下一关,假定某选手获得面试资格的概率与答对每道题的概率相等.
 求该选手答完3道题而通过第一关的概率;
求该选手答完3道题而通过第一关的概率; 记该选手在面试第一关中的答题个数为X,求X的分布列及数学期望.
记该选手在面试第一关中的答题个数为X,求X的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数
 .
.(1)讨论
 的单调性;
的单调性;(2)设
 ,证明:
,证明:  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:点P在直径AB=1的半圆上移动(点P不与A,B重合),过P作圆的切线PT且PT=1,∠PAB=α,
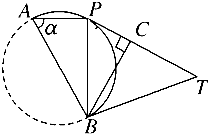
(1)当α为何值时,四边形ABTP面积最大?
(2)求|PA|+|PB|+|PC|的取值范围? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若不等式
 的解集为
的解集为 ,求实数
,求实数 的值;
的值;(2)在(1)的条件下,若存在实数
 使
使 成立,求实数
成立,求实数 的取值范围.
的取值范围.
相关试题

