【题目】下列命题正确的序号为______.

①周期函数都有最小正周期；②偶函数一定不存在反函数；

③“是单调函数”是“存在反函数”的充分不必要条件；

④若原函数与反函数的图像有偶数个交点，则可能都不在直线上；

参考答案：

【答案】③④

【解析】

根据题意，对题目中的命题进行分析、判断真假性即可．

对于①，不是所有的周期函数都有最小正周期，如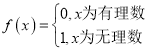，①错误；

对于②，，，是偶函数，它有反函数，②错误；

对于③，是单调函数时，存在反函数，充分性成立，

存在反函数时，不一定是单调函数，如，，必要性不成立，

是充分不必要条件，③正确；

对于④，原函数与反函数的图象有偶数个交点时，则它们的交点必关于直线对称，

也可能都不在直线上，④正确；

综上所述，正确的命题序号是③④．

故答案为：③④．

关闭