【题目】某大学准备在开学时举行一次大学一年级学生座谈会,拟邀请20名来自本校机械工程学院、海洋学院、医学院、经济学院的学生参加,各学院邀请的学生数如下表所示:
学院 | 机械工程学院 | 海洋学院 | 医学院 | 经济学院 |
人数 | 4 | 6 | 4 | 6 |
(Ⅰ)从这20名学生中随机选出3名学生发言,求这3名学生中任意两个均不属于同一学院的概率;
(Ⅱ)从这20名学生中随机选出3名学生发言,设来自医学院的学生数为ξ,求随机变量ξ的概率分布列和数学期望.
参考答案:
【答案】解:(Ⅰ)从20名学生随机选出3名的方法数为 ![]() ,
,
选出3人中任意两个均不属于同一学院的方法数为:![]()
所以 ![]()
(Ⅱ)ξ可能的取值为0,1,2,3,![]() ,
, ![]()
所以ξ的分布列为
0 | 1 | 2 | 3 | |
P |
|
|
|
|
所以 ![]()
【解析】(Ⅰ)从20名学生随机选出3名的方法数为 ![]() ,选出3人中任意两个均不属于同一学院的方法数为
,选出3人中任意两个均不属于同一学院的方法数为 ![]() ,由此利用等可能事件概率计算公式能求出这3名学生中任意两个均不属于同一学院的概率.(Ⅱ)ξ可能的取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量ξ的概率分布列和数学期望.
,由此利用等可能事件概率计算公式能求出这3名学生中任意两个均不属于同一学院的概率.(Ⅱ)ξ可能的取值为0,1,2,3,分别求出相应的概率,由此能求出随机变量ξ的概率分布列和数学期望.
【考点精析】通过灵活运用离散型随机变量及其分布列,掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1),r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则( )
A. r2<0<r1 B. 0<r2<r1 C. r2<r1<0 D. r2=r1
-
科目: 来源: 题型:
查看答案和解析>>【题目】若执行下面的程序框图,输出
 的值为3,则判断框中应填入的条件是( )
的值为3,则判断框中应填入的条件是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的序号为______.
①周期函数都有最小正周期;②偶函数一定不存在反函数;
③“
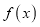 是单调函数”是“
是单调函数”是“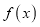 存在反函数”的充分不必要条件;
存在反函数”的充分不必要条件;④若原函数与反函数的图像有偶数个交点,则可能都不在直线
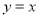 上;
上; -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.
(Ⅰ)若BM=2MP,求证:PD∥平面MAC;
(Ⅱ)若平面PAB⊥平面ABCD,平面PAD⊥平面ABCD,求证:PA⊥平面ABCD;
(Ⅲ)在(Ⅱ)的条件下,若二面角B﹣AC﹣M的余弦值为 ,求
,求  的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面几何中,可以得出正确结论:“正三角形的内切圆半径等于这个正三角形的高的
 .”拓展到空间中,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的( )
.”拓展到空间中,类比平面几何的上述结论,则正四面体的内切球半径等于这个正四面体的高的( )A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}是等差数列,Sn为{an}的前n项和,且a10=19,S10=100;数列{bn}对任意n∈N* , 总有b1b2b3…bn﹣1bn=an+2成立.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记cn=(﹣1)n ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
相关试题

