【题目】已知函数![]() .
.
![]() Ⅰ
Ⅰ![]() 若函数
若函数![]() 在区间
在区间![]() 上为增函数,求a的取值范围;
上为增函数,求a的取值范围;
![]() Ⅱ
Ⅱ![]() 若对任意
若对任意![]() 恒成立,求实数m的最大值.
恒成立,求实数m的最大值.
参考答案:
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)g(x)的导数导数大于或等于0恒成立,转化成求不等式恒成立问题
(2) 求不等式恒成立问题转化成求最值问题,利用导数知识判断函数的单调性,从而求最值。
(1)由题意得g′(x)=f′(x)+a=ln x+a+1.
∵函数g(x)在区间[e2,+∞)上为增函数,∴当x∈[e2,+∞)时,g′(x)≥0,
即ln x+a+1≥0在[e2,+∞)上恒成立.∴a≥-1-ln x.
令h(x)=-ln x-1,∴a≥h(x)max,
当x∈[e2,+∞)时,ln x∈[2,+∞),
∴h(x)∈(-∞,-3],∴a≥-3,
即实数a的取值范围是[-3,+∞).
(2)∵2f(x)≥-x2+mx-3,即mx≤2xln x+x2+3,
又x>0,∴m≤![]() 在x∈(0,+∞)上恒成立.
在x∈(0,+∞)上恒成立.
记t(x)=![]() =2ln x+x+
=2ln x+x+![]() .∴m≤t(x)min.
.∴m≤t(x)min.
∵t′(x)=![]() +1-
+1-![]() =
=![]() =
=![]() ,
,
令t′(x)=0,得x=1或x=-3(舍去).
当x∈(0,1)时,t′(x)<0,函数t(x)在(0,1)上单调递减;
当x∈(1,+∞)时,t′(x)>0,函数t(x)在(1,+∞)上单调递增,∴t(x)min=t(1)=4.
∴m≤t(x)min=4,即m的最大值为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2019年4月,河北、辽宁、江苏、福建、湖北、湖南、广东、重庆等8省市发布高考综合改革实施方案,决定从2018年秋季入学的高中一年级学生开始实施“
 ”高考模式.所谓“
”高考模式.所谓“ ”,即“3”是指考生必选语文、数学、外语这三科;“1”是指考生在物理、历史两科中任选一科;“2”是指考生在生物、化学、思想政治、地理四科中任选两科.
”,即“3”是指考生必选语文、数学、外语这三科;“1”是指考生在物理、历史两科中任选一科;“2”是指考生在生物、化学、思想政治、地理四科中任选两科.(1)若某考生按照“
 ”模式随机选科,求选出的六科中含有“语文,数学,外语,物理,化学”的概率.
”模式随机选科,求选出的六科中含有“语文,数学,外语,物理,化学”的概率.(2)新冠疫情期间,为积极应对“
 ”新高考改革,某地高一年级积极开展线上教学活动.教育部门为了解线上教学效果,从当地不同层次的学校中抽取高一学生2500名参加语数外的网络测试,并给前400名颁发荣誉证书,假设该次网络测试成绩服从正态分布,且满分为450分.
”新高考改革,某地高一年级积极开展线上教学活动.教育部门为了解线上教学效果,从当地不同层次的学校中抽取高一学生2500名参加语数外的网络测试,并给前400名颁发荣誉证书,假设该次网络测试成绩服从正态分布,且满分为450分.①考生甲得知他的成绩为270分,考试后不久了解到如下情况:“此次测试平均成绩为171分,351分以上共有57人”,请用你所学的统计知识估计甲能否获得荣誉证书,并说明理由;
②考生丙得知他的实际成绩为430分,而考生乙告诉考生丙:“这次测试平均成绩为201分,351分以上共有57人”,请结合统计学知识帮助丙同学辨别乙同学信息的真伪,并说明理由.
附:
 ;
; ;
; .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为迎接中华人民共和国成立
 周年,开展了以“厉害了,我的国”为主题的征文比赛,评选出一、二、三等奖和优秀奖.校团委根据获奖的结果绘制成了如下两幅不完整的统计图:
周年,开展了以“厉害了,我的国”为主题的征文比赛,评选出一、二、三等奖和优秀奖.校团委根据获奖的结果绘制成了如下两幅不完整的统计图:
(1)扇形统计图中三等奖所在扇形的圆心角的度数是__________度;
(2)请补全条形统计图;
(3)在此次征文比赛中,获得“一等奖”的同学中有两人来自初三年级.现要从获得“一等奖”同学中随机抽选两人参加该校团委组织的征文比赛总结会,请用画树状图或列表法求选中的两人刚好都来自初三年级的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
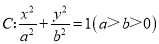 的左、右焦点分别为F1,F2,过点F1的直线与C交于A,B两点.△ABF2的周长为
的左、右焦点分别为F1,F2,过点F1的直线与C交于A,B两点.△ABF2的周长为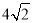 ,且椭圆的离心率为
,且椭圆的离心率为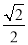 .
.(1)求椭圆C的标准方程:
(2)设点P为椭圆C的下顶点,直线PA,PB与y=2分别交于点M,N,当|MN|最小时,求直线AB的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,直线
 的参数方程为
的参数方程为 ,(
,( 为参数).以原点为极点,
为参数).以原点为极点, 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)写出直线
 的极坐标方程与曲线
的极坐标方程与曲线 的直角坐标方程;
的直角坐标方程;(2)已知与直线
 平行的直线
平行的直线 过点
过点 ,且与曲线
,且与曲线 交于
交于 两点,试求
两点,试求 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,椭圆
,椭圆 :
: 与双曲线
与双曲线 :
: 的焦点相同.
的焦点相同.(1)求椭圆
 与双曲线
与双曲线 的方程;
的方程;(2)过双曲线
 的右顶点作两条斜率分别为
的右顶点作两条斜率分别为 ,
, 的直线
的直线 ,
, ,分别交双曲线
,分别交双曲线 于点
于点 ,
, (
( ,
, 不同于右顶点),若
不同于右顶点),若 ,求证:直线
,求证:直线 的倾斜角为定值,并求出此定值;
的倾斜角为定值,并求出此定值;(3)设点
 ,若对于直线
,若对于直线 ,椭圆
,椭圆 上总存在不同的两点
上总存在不同的两点 与
与 关于直线
关于直线 对称,且
对称,且 ,求实数
,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】将
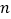 个数
个数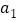 ,
,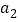 ,…,
,…,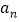 的连乘积
的连乘积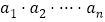 记为
记为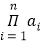 ,将
,将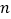 个数
个数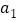 ,
,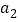 ,…,
,…,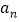 的和
的和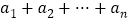 记为
记为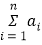 .(
.(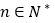 )
)(1)若数列
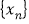 满足
满足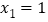 ,
,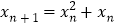 ,
,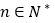 ,设
,设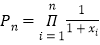 ,
,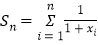 ,求
,求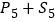 ;
;(2)用
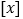 表示不超过
表示不超过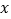 的最大整数,例如
的最大整数,例如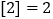 ,
, ,
,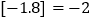 .若数列
.若数列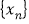 满足
满足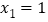 ,
,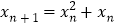 ,
,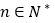 ,求
,求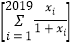 的值;
的值;(3)设定义在正整数集
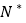 上的函数
上的函数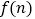 满足:当
满足:当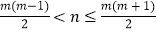 (
(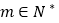 )时,
)时,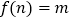 ,问是否存在正整数
,问是否存在正整数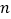 ,使得
,使得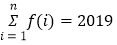 ?若存在,求出
?若存在,求出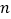 的值;若不存在,说明理由(已知
的值;若不存在,说明理由(已知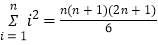 ).
).
相关试题

