【题目】给定区域D:  .令点集T={(x0 , y0)∈D|x0 , y0∈Z,(x0 , y0)是z=x+y在D上取得最大值或最小值的点},则T中的点共确定条不同的直线.
.令点集T={(x0 , y0)∈D|x0 , y0∈Z,(x0 , y0)是z=x+y在D上取得最大值或最小值的点},则T中的点共确定条不同的直线.
参考答案:
【答案】6
【解析】解:画出不等式表示的平面区域,如图.
作出目标函数对应的直线,因为直线z=x+y与直线x+y=4平行,故直线z=x+y过直线x+y=4上的整数点:(4,0),(3,1),(2,2),(1,3)或(0,4)时,直线的纵截距最大,z最大;
当直线过(0,1)时,直线的纵截距最小,z最小,从而点集T={(4,0),(3,1),(2,2),(1,3),(0,4),(0,1)},经过这六个点的直线一共有6条.
即T中的点共确定6条不同的直线.
所以答案是:6.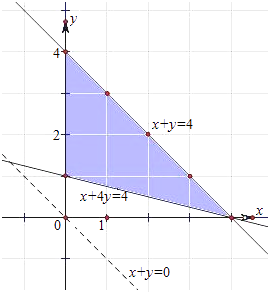
-
科目: 来源: 题型:
查看答案和解析>>【题目】某个产品有若干零部件构成,加工时需要经过7道工序,分别记为
 .其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系,若加工工序
.其中,有些工序因为是制造不同的零部件,所以可以在几台机器上同时加工;有些工序因为是对同一个零部件进行处理,所以存在加工顺序关系,若加工工序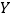 必须要在工序
必须要在工序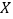 完成后才能开工,则称
完成后才能开工,则称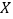 为
为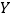 的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:
的紧前工序.现将各工序的加工次序及所需时间(单位:小时)列表如下:工序







加工时间
3
4
2
2
2
1
5
紧前工序
无

无




现有两台性能相同的生产机器同时加工该产品,则完成该产品的最短加工时间是( )
(假定每道工序只能安排在一台机器上,且不能间断.)
A. 11个小时 B. 10个小时 C. 9个小时 D. 8个小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电影院共有
 个座位,某天,这家电影院上、下午各演一场电影.看电影的是甲、乙、丙三所中学的学生,三所学校的观影人数分别是985人,1010人,2019人(同一所学校的学生既可看上午场,又可看下午场,但每人只能看一场).已知无论如何排座位,这天观影时总存在这样的一个座位,上、下午在这个座位上坐的是同一所学校的学生,那么
个座位,某天,这家电影院上、下午各演一场电影.看电影的是甲、乙、丙三所中学的学生,三所学校的观影人数分别是985人,1010人,2019人(同一所学校的学生既可看上午场,又可看下午场,但每人只能看一场).已知无论如何排座位,这天观影时总存在这样的一个座位,上、下午在这个座位上坐的是同一所学校的学生,那么 的可能取值有__________个.
的可能取值有__________个. -
科目: 来源: 题型:
查看答案和解析>>【题目】在奥运知识有奖问答竞赛中,甲、乙、丙三人同时回答一道有关奥运知识的问题,已知甲答对这道题的概率是
 ,甲、乙两人都回答错误的概率是
,甲、乙两人都回答错误的概率是 ,乙、丙两人都回答正确的概率是
,乙、丙两人都回答正确的概率是 .设每人回答问题正确与否相互独立的.
.设每人回答问题正确与否相互独立的.(Ⅰ)求乙答对这道题的概率;
(Ⅱ)求甲、乙、丙三人中,至少有一人答对这道题的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
 ,函数
,函数 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减.
上单调递减.(Ⅰ)若
 ,求
,求 的值;
的值;(Ⅱ)求函数
 在区间
在区间 上的最小值(用
上的最小值(用 表示).
表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标
 中,圆
中,圆 与圆
与圆 相交与
相交与 两点.
两点.(I)求线段
 的长.
的长.(II)记圆
 与
与 轴正半轴交于点
轴正半轴交于点 ,点
,点 在圆C上滑动,求
在圆C上滑动,求 面积最大时的直线
面积最大时的直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个篮球队在4次不同比赛中的得分情况如下:
甲队
88
91
92
96
乙队
89
93
9▓
92
乙队记录中有一个数字模糊(即表中阴影部分),无法确认,假设这个数字具有随机性,并用
 表示.
表示.(Ⅰ)在4次比赛中,求乙队平均得分超过甲队平均得分的概率;
(Ⅱ)当
 时,分别从甲、乙两队的4次比赛中各随机选取1次,记这2个比赛得分之差的绝对值为
时,分别从甲、乙两队的4次比赛中各随机选取1次,记这2个比赛得分之差的绝对值为 ,求随机变量
,求随机变量 的分布列;
的分布列;(Ⅲ)如果乙队得分数据的方差不小于甲队得分数据的方差,写出
 的取值集合.(结论不要求证明)
的取值集合.(结论不要求证明)
相关试题

