Question

【题目】甲、乙两个篮球队在4次不同比赛中的得分情况如下：

甲队	88	91	92	96
乙队	89	93	9▓	92

乙队记录中有一个数字模糊（即表中阴影部分），无法确认，假设这个数字具有随机性，并用表示.

（Ⅰ）在4次比赛中，求乙队平均得分超过甲队平均得分的概率；

（Ⅱ）当时，分别从甲、乙两队的4次比赛中各随机选取1次，记这2个比赛得分之差的绝对值为，求随机变量的分布列；

（Ⅲ）如果乙队得分数据的方差不小于甲队得分数据的方差，写出的取值集合.(结论不要求证明）

Answer 1

【答案】（Ⅰ）；（Ⅱ）分布列见解析；（Ⅲ）.

【解析】分析：（Ⅰ）根据表中数据，写出的全部可能，求甲、乙队的平均成绩，列出关于的不等式，求出的取值集合，再由古典概型的概率计算公式求出答案.

（Ⅱ）2个比赛得分之差的绝对值的所有取值为0，1，2，3，4，5，7，求出相应概率，即可求出随机变量的分布列.

（Ⅲ）写出甲、乙两队的方差，列出关于的不等式，即可求出的取值集合.

详解：解：（Ⅰ）设“乙队平均得分超过甲队平均得分”为事件,

依题意，共有10种可能.

由乙队平均得分超过甲队平均得分，得

解得

所以当时，乙队平均得分超过甲队平均得分，共6种可能.

所以乙队平均得分超过甲队平均得分的概率为

（Ⅱ）当时，记甲队的4次比赛得分88，91，92，96分别为，乙队的4次比赛得分89，93，95，92分别为

则分别从甲、乙两队的4次比赛中各随机选取1次，所有可能的得分结果有种，它们是

则这2个比赛得分之差的绝对值为的所有取值为0，1，2，3，4，5，7.

因此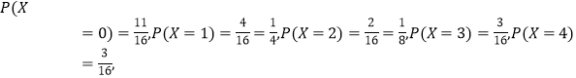

所以随机变量的分布为：

	0	1	2	3	4	5	7

(Ⅲ）