【题目】设函数f(x)=|2x+1|﹣|x﹣4|.
(1)解不等式f(x)>0;
(2)若f(x)+3|x﹣4|>m对一切实数x均成立,求m的取值范围.
参考答案:
【答案】
(1)
解:当x≥4时f(x)=2x+1﹣(x﹣4)=x+5>0得 x>﹣5,所以,x≥4时,不等式成立.
当 ![]() 时,f(x)=2x+1+x﹣4=3x﹣3>0,得x>1,所以,1<x<4时,不等式成立.
时,f(x)=2x+1+x﹣4=3x﹣3>0,得x>1,所以,1<x<4时,不等式成立.
当 ![]() 时,f(x)=﹣x﹣5>0,得x<﹣5,所以,x<﹣5成立
时,f(x)=﹣x﹣5>0,得x<﹣5,所以,x<﹣5成立
综上,原不等式的解集为:{x|x>1或x<﹣5}
(2)
解:f(x)+3|x﹣4|=|2x+1|+2|x﹣4|≥|2x+1﹣(2x﹣8)|=9,当且仅当﹣ ![]() ≤x≤4时,取等号,
≤x≤4时,取等号,
所以,f(x)+3|x﹣4|的最小值为9,故 m<9
【解析】(1)分类讨论,当x≥4时,当 ![]() 时,当
时,当 ![]() 时,分别求出不等式的解集,再把解集取交集.(2)利用绝对值的性质,求出f(x)+3|x﹣4|的最小值为9,故m<9.
时,分别求出不等式的解集,再把解集取交集.(2)利用绝对值的性质,求出f(x)+3|x﹣4|的最小值为9,故m<9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
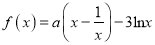 .
.(1)若函数
 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数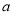 的取值范围;
的取值范围;(3)设函数
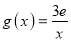 ,若在
,若在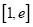 上至少存在一点
上至少存在一点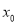 ,使得
,使得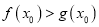 成立,求实数
成立,求实数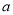 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列
 中,
中,  ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数,  ,且
,且 ,
,  .
.(1)求数列
 和
和 的通项公式;
的通项公式;(2)令
 ,设数列
,设数列 的前
的前 项和为
项和为 ,求
,求 (
( )的最大值与最小值.
)的最大值与最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
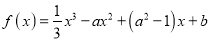 (
(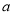 ,
, 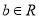 ).
).(1)若
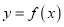 的图象在点
的图象在点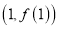 处的切线方程为
处的切线方程为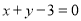 ,求
,求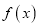 在区间
在区间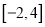 上的最大值和最小值;
上的最大值和最小值;(2)若
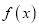 在区间
在区间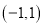 上不是单调函数,求
上不是单调函数,求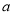 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中,以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=4sinθ.
(1)求曲线C的直角坐标方程;
(2)若曲线C1: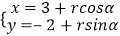 (α为参数)与曲线C所表示的图形都相切,求r的值.
(α为参数)与曲线C所表示的图形都相切,求r的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x∈R,[x]表示不超过x的最大整数,若函数
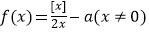 有且仅有3个零点,则实数a的取值范围是.
有且仅有3个零点,则实数a的取值范围是. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
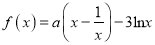 .
.(1)若函数
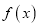 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数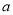 的取值范围;
的取值范围;(3)设函数
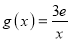 ,若在
,若在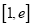 上至少存在一点
上至少存在一点 ,使得
,使得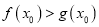 成立,求实数
成立,求实数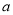 的取值范围.
的取值范围.
相关试题

