【题目】已知函数![]() .
.
(1)若函数![]() 在其定义域内为增函数,求实数
在其定义域内为增函数,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,若在
,若在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由题意得导函数在其定义域内恒非负,再根据二次方程恒成立条件得实数![]() 的取值范围;(2)将不等式有解问题,利用参变分离法转化为对应函数最值问题,再利用导数求对应函数最值,即得实数
的取值范围;(2)将不等式有解问题,利用参变分离法转化为对应函数最值问题,再利用导数求对应函数最值,即得实数![]() 的取值范围.
的取值范围.
试题解析:(1)![]() ,
, ![]() ,
,
因为函数![]() 在其定义域内为增函数,
在其定义域内为增函数,
所以![]() ,
, ![]() 恒成立,
恒成立,
当![]() 时,显然不成立;
时,显然不成立;
当![]() 时,
时, ![]() ,要满足
,要满足![]() ,
, ![]() 时恒成立,则
时恒成立,则![]() ,
,
∴![]() .
.
(2)设函数![]() ,
, ![]() ,
,
则原问题转化为在![]() 上至少存在一点
上至少存在一点![]() ,使得
,使得![]() ,即
,即![]() .
.
①![]() 时,
时, ![]() ,
,
∵![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() ,则
,则![]() ,不符合条件;
,不符合条件;
②![]() 时,
时, ![]() ,
,
由![]() ,可知
,可知![]() ,
,
则![]() 在
在![]() 单调递增,
单调递增, ![]() ,整理得
,整理得![]() .
.
综上所述, ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:x2+y2﹣2x﹣2ay+a2﹣24=0(a∈R)的圆心在直线2x﹣y=0上.
(1)求实数a的值;
(2)求圆C与直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R)相交弦长的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查某高中学生每天的睡眠时间,现随机对20名男生和20名女生进行问卷调查,结果如下:
女生:睡眠时间(小时)
[4,5)
[5,6)
[6,7)
[7,8)
[8,9]
人数
2
4
8
4
2
男生:
睡眠时间(小时)
[4,5)
[5,6)
[6,7)
[7,8)
[8,9]
人数
1
5
6
5
3
(1)现把睡眠时间不足5小时的定义为“严重睡眠不足”,从睡眠时间不足6小时的女生中随机抽取2人,求此2人中恰有一人为“严重睡眠不足”的概率;
(2)完成下面2×2列联表,并回答是否有90%的把握认为“睡眠时间与性别有关”?睡眠时间少于7小时
睡眠时间不少于7小时
合计
男生
女生
合计
P(K2≥k)
0.15
0.10
0.05
0.025
0.010
0.005
0.001
k
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(
 ,其中n=a+b+c+d)
,其中n=a+b+c+d) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为(﹣∞,0)∪(0,+∞),f(x)是奇函数,且当x>0时,f(x)=x2﹣x+a,若函数g(x)=f(x)﹣x的零点恰有两个,则实数a的取值范围是( )
A.a<0
B.a≤0
C.a≤1
D.a≤0或a=1 -
科目: 来源: 题型:
查看答案和解析>>【题目】在等差数列
 中,
中,  ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数,  ,且
,且 ,
,  .
.(1)求数列
 和
和 的通项公式;
的通项公式;(2)令
 ,设数列
,设数列 的前
的前 项和为
项和为 ,求
,求 (
( )的最大值与最小值.
)的最大值与最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
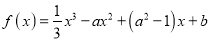 (
(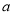 ,
, 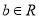 ).
).(1)若
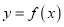 的图象在点
的图象在点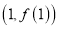 处的切线方程为
处的切线方程为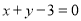 ,求
,求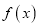 在区间
在区间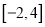 上的最大值和最小值;
上的最大值和最小值;(2)若
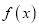 在区间
在区间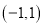 上不是单调函数,求
上不是单调函数,求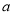 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|2x+1|﹣|x﹣4|.
(1)解不等式f(x)>0;
(2)若f(x)+3|x﹣4|>m对一切实数x均成立,求m的取值范围.
相关试题

