【题目】如图,在多面体![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,四边形
,四边形![]() 是矩形,平面
是矩形,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 是
是![]() 的中点.
的中点.

(1)求证: ![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(3)求二面角![]() 的大小.
的大小.
参考答案:
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)由平面![]() 平面
平面![]() ,及
,及![]() ,得
,得![]() 平面
平面![]() (平面与平面垂直的性质);(2)建立适当的空间直角坐标系,求得平面
(平面与平面垂直的性质);(2)建立适当的空间直角坐标系,求得平面![]() 的法向量的坐标及
的法向量的坐标及![]() ,可得
,可得![]() 与平面
与平面![]() 所成角的夹角的正弦值;(3)由(2)的空间直角坐标,可求得
所成角的夹角的正弦值;(3)由(2)的空间直角坐标,可求得![]() 的法向量
的法向量![]() ,平面
,平面![]() 的法向量
的法向量![]() ,得
,得![]() ,由二面角为锐角,得所求二面角的值。
,由二面角为锐角,得所求二面角的值。
(1)证明:因为四边形![]() 是菱形,所以
是菱形,所以![]() .
.
因为平面![]() 平面
平面![]() ,且四边形
,且四边形![]() 是矩形,所以
是矩形,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)设![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
因为四边形![]() 是矩形,
是矩形, ![]() 分别为
分别为![]() ,
, ![]() 的中点,所以
的中点,所以![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
由![]() ,得
,得![]() 两两垂直,所以以
两两垂直,所以以![]() 为原点,
为原点, ![]() 所在直线分别为
所在直线分别为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.
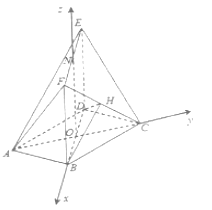
因为底面![]() 是边长为
是边长为![]() 的菱形,
的菱形, ![]() ,
, ![]() ,
,
所以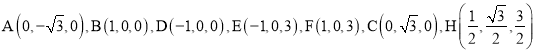 .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 的法向量
的法向量![]() .
.
设直线![]() 与平面
与平面![]() 所成角为
所成角为![]() ,由
,由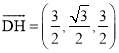 ,得
,得
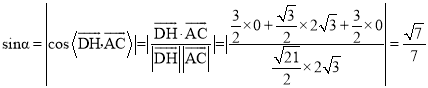 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(3)由(2)得, 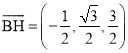 ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
所以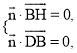 即
即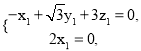
令![]() ,得
,得![]() ,由
,由![]() 平面
平面![]() ,得平面
,得平面![]() 的法向量为
的法向量为![]() ,
,
则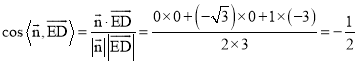 ,
,
由图可知二面角![]() 为锐角,
为锐角,
所以二面角![]() 的大小为
的大小为![]() .
.
-
科目: 来源: 题型:
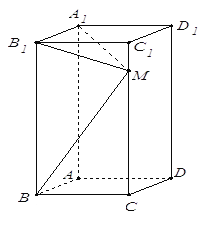
查看答案和解析>>【题目】如图所示,在长方体
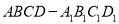 中,
中,  ,
, 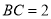 ,
, 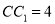 ,
, 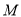 为棱
为棱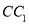 上一点,
上一点,(1)若
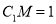 ,求异面直线
,求异面直线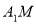 和
和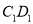 所成角的正切值;
所成角的正切值;(2)若
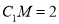 ,求证
,求证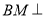 平面
平面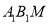 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
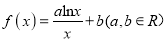 的图像在点
的图像在点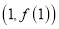 处的切线方程为
处的切线方程为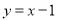 .
.(1)求实数
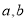 的值及函数
的值及函数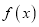 的单调区间;
的单调区间;(2)当
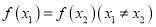 时,比较
时,比较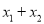 与
与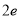 (
(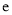 为自然对数的底数)的大小.
为自然对数的底数)的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足:a1=1,a2=2,且an+1=2an+3an﹣1(n≥2,n∈N+).
(1)设bn=an+1+an(n∈N+),求证{bn}是等比数列;
(2)(i)求数列{an}的通项公式;
(ii)求证:对于任意n∈N+都有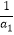 +
+ 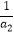 +…+
+…+ 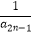 +
+ 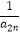 <
<  成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,若acosA﹣bcosB=0,则三角形的形状是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
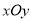 中,以原点
中,以原点 为极点,
为极点, 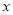 轴的正半轴为极轴,建立极坐标系.已知点
轴的正半轴为极轴,建立极坐标系.已知点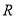 的极坐标为
的极坐标为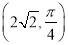 ,曲线
,曲线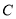 的参数方程为
的参数方程为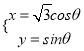 (
(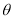 为参数)
为参数)(1)求点
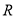 的直角坐标;化曲线
的直角坐标;化曲线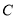 的参数方程为普通方程;
的参数方程为普通方程;(2)设
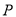 为曲线
为曲线 上一动点,以
上一动点,以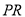 为对角线的矩形
为对角线的矩形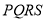 的一边垂直于极轴,求矩形
的一边垂直于极轴,求矩形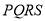 周长的最小值,及此时
周长的最小值,及此时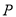 点的直角坐标.
点的直角坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形
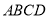 四点坐标为A(0,-2),C(4,2),B(4,-2),D(0,2).
四点坐标为A(0,-2),C(4,2),B(4,-2),D(0,2).
(1)求对角线
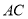 所在直线的方程;
所在直线的方程;(2)求矩形
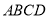 外接圆的方程;
外接圆的方程;(3)若动点
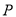 为外接圆上一点,点
为外接圆上一点,点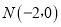 为定点,问线段PN中点的轨迹是什么,并求出该轨迹方程。
为定点,问线段PN中点的轨迹是什么,并求出该轨迹方程。
相关试题

