【题目】在△ABC中,若acosA﹣bcosB=0,则三角形的形状是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
参考答案:
【答案】D
【解析】解:法1:∵cosA= ![]() ,cosB=
,cosB= ![]() , ∴
, ∴ ![]() a=
a= ![]() b,
b,
化简得:a2c2﹣a4=b2c2﹣b4 , 即(a2﹣b2)c2=(a2﹣b2)(a2+b2),
①若a2﹣b2=0时,a=b,此时△ABC是等腰三角形;
②若a2﹣b2≠0,a2+b2=c2 , 此时△ABC是直角三角形,
所以△ABC是等腰三角形或直角三角形;
法2:根据正弦定理可知∵acosA=bcosB,
∴sinAcosA=sinBcosB,
∴sin2A=sin2B,
∴A=B,或2A+2B=180°即A+B=90°,
所以△ABC为等腰或直角三角形.
故选D
解法1:把由余弦定理解出的余弦表达式代入已知的等式化简可得:(a2﹣b2)c2=(a2﹣b2)(a2+b2),分①a2﹣b2=0和②a2﹣b2≠0两种情况讨论;
解法2:根据正弦定理把等式acosA=bcosB的边换成角的正弦,再利用倍角公式化简整理得sin2A=sin2B,进而推断A=B,或A+B=90°答案可得.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
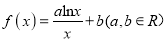 的图像在点
的图像在点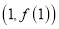 处的切线方程为
处的切线方程为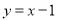 .
.(1)求实数
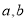 的值及函数
的值及函数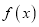 的单调区间;
的单调区间;(2)当
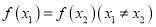 时,比较
时,比较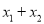 与
与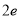 (
(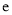 为自然对数的底数)的大小.
为自然对数的底数)的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足:a1=1,a2=2,且an+1=2an+3an﹣1(n≥2,n∈N+).
(1)设bn=an+1+an(n∈N+),求证{bn}是等比数列;
(2)(i)求数列{an}的通项公式;
(ii)求证:对于任意n∈N+都有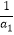 +
+ 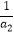 +…+
+…+ 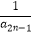 +
+ 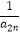 <
<  成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在多面体
 中,底面
中,底面 是边长为
是边长为 的菱形,
的菱形,  ,四边形
,四边形 是矩形,平面
是矩形,平面 平面
平面 ,
,  ,
,  是
是 的中点.
的中点.
(1)求证:
 平面
平面 ;
;(2)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)求二面角
 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
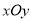 中,以原点
中,以原点 为极点,
为极点, 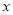 轴的正半轴为极轴,建立极坐标系.已知点
轴的正半轴为极轴,建立极坐标系.已知点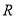 的极坐标为
的极坐标为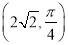 ,曲线
,曲线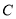 的参数方程为
的参数方程为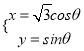 (
(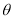 为参数)
为参数)(1)求点
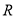 的直角坐标;化曲线
的直角坐标;化曲线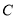 的参数方程为普通方程;
的参数方程为普通方程;(2)设
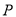 为曲线
为曲线 上一动点,以
上一动点,以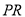 为对角线的矩形
为对角线的矩形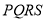 的一边垂直于极轴,求矩形
的一边垂直于极轴,求矩形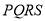 周长的最小值,及此时
周长的最小值,及此时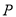 点的直角坐标.
点的直角坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知矩形
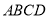 四点坐标为A(0,-2),C(4,2),B(4,-2),D(0,2).
四点坐标为A(0,-2),C(4,2),B(4,-2),D(0,2).
(1)求对角线
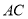 所在直线的方程;
所在直线的方程;(2)求矩形
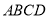 外接圆的方程;
外接圆的方程;(3)若动点
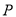 为外接圆上一点,点
为外接圆上一点,点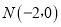 为定点,问线段PN中点的轨迹是什么,并求出该轨迹方程。
为定点,问线段PN中点的轨迹是什么,并求出该轨迹方程。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
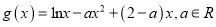 .
.(1)求
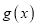 的单调区间;
的单调区间;(2)若函数
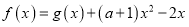 ,
, 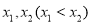 是函数
是函数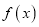 的两个零点,
的两个零点, 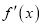 是函数
是函数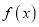 的导函数,证明:
的导函数,证明: 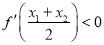 .
.
相关试题

