【题目】已知数列{an}满足:a1=1,a2=2,且an+1=2an+3an﹣1(n≥2,n∈N+).
(1)设bn=an+1+an(n∈N+),求证{bn}是等比数列;
(2)(i)求数列{an}的通项公式;
(ii)求证:对于任意n∈N+都有 ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]() <
< ![]() 成立.
成立.
参考答案:
【答案】
(1)证明:已知数列{an}满足:a1=1,a2=2,且an+1=2an+3an﹣1(n≥2,n∈N+).
则:an+1+an=3(an+an﹣1)
即: ![]() ,
,
所以: ![]() ,
,
数列{bn}是等比数列.
(2)解:(i)由于数列{bn}是等比数列.
则: ![]() ,
,
整理得: ![]()
所以: ![]()
则: ![]() 是以(
是以( ![]() )为首项,﹣1为公比的等比数列.
)为首项,﹣1为公比的等比数列.
所以: ![]()
求得: ![]()
(ii)由于: ![]() ,
,
所以: ![]() ,
,
则:(1)当n为奇数时, ![]() ,
,
当n为偶数时, ![]() ,
,
所以: ![]() =
= ![]() …+
…+ ![]() +
+ ![]()
![]() ,
,
所以:n∈k时,对任意的k都有 ![]() 恒成立
恒成立
【解析】(1)利用已知条件对已知的数列关系式进行恒等变形,进一步的出数列是等比数列.(2)(i)根据(1)的结论进一步利用恒等变换,求出数列的通项公式.(ii)首先分奇数和偶数分别写出通项公式,进一步利用放缩法进行证明.
【考点精析】本题主要考查了等比关系的确定和数列的前n项和的相关知识点,需要掌握等比数列可以通过定义法、中项法、通项公式法、前n项和法进行判断;数列{an}的前n项和sn与通项an的关系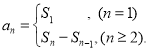 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
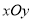 中,已知曲线
中,已知曲线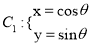 (
(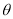 为参数),将
为参数),将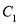 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的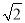 和
和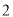 倍后得到曲线
倍后得到曲线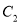 .以平面直角坐标系
.以平面直角坐标系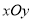 的原点
的原点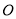 为极点,
为极点, 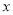 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线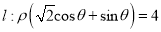 .
.(1)试写出曲线
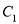 的极坐标方程与曲线
的极坐标方程与曲线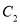 的参数方程;
的参数方程;(2)在曲线
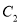 上求一点
上求一点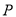 ,使点
,使点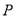 到直线
到直线 的距离最小,并求此最小值.
的距离最小,并求此最小值. -
科目: 来源: 题型:
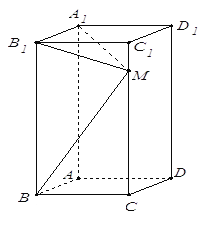
查看答案和解析>>【题目】如图所示,在长方体
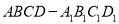 中,
中,  ,
, 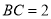 ,
, 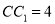 ,
, 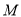 为棱
为棱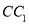 上一点,
上一点,(1)若
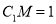 ,求异面直线
,求异面直线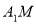 和
和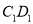 所成角的正切值;
所成角的正切值;(2)若
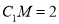 ,求证
,求证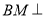 平面
平面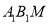 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
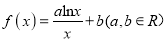 的图像在点
的图像在点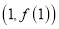 处的切线方程为
处的切线方程为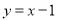 .
.(1)求实数
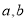 的值及函数
的值及函数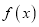 的单调区间;
的单调区间;(2)当
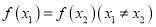 时,比较
时,比较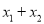 与
与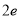 (
(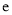 为自然对数的底数)的大小.
为自然对数的底数)的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在多面体
 中,底面
中,底面 是边长为
是边长为 的菱形,
的菱形,  ,四边形
,四边形 是矩形,平面
是矩形,平面 平面
平面 ,
,  ,
,  是
是 的中点.
的中点.
(1)求证:
 平面
平面 ;
;(2)求直线
 与平面
与平面 所成角的正弦值;
所成角的正弦值;(3)求二面角
 的大小.
的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,若acosA﹣bcosB=0,则三角形的形状是( )
A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在直角坐标系
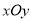 中,以原点
中,以原点 为极点,
为极点, 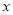 轴的正半轴为极轴,建立极坐标系.已知点
轴的正半轴为极轴,建立极坐标系.已知点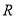 的极坐标为
的极坐标为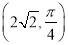 ,曲线
,曲线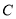 的参数方程为
的参数方程为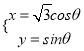 (
(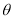 为参数)
为参数)(1)求点
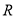 的直角坐标;化曲线
的直角坐标;化曲线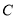 的参数方程为普通方程;
的参数方程为普通方程;(2)设
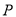 为曲线
为曲线 上一动点,以
上一动点,以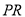 为对角线的矩形
为对角线的矩形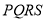 的一边垂直于极轴,求矩形
的一边垂直于极轴,求矩形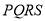 周长的最小值,及此时
周长的最小值,及此时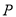 点的直角坐标.
点的直角坐标.
相关试题

