【题目】如表中给出了2011年~2015年某市快递业务总量的统计数据(单位:百万件)
年份 | 2011 | 2012 | 2013 | 2014 | 2015 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
快递业务总量 | 34 | 55 | 71 | 85 | 105 |
(1)在图中画出所给数据的折线图; 
(2)建立一个该市快递量y关于年份代码x的线性回归模型;
(3)利用(2)所得的模型,预测该市2016年的快递业务总量.
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:
斜率: 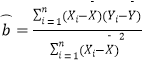 ,纵截距:
,纵截距: ![]() .
.
参考答案:
【答案】
(1)解:所给数据的折线图如下:

…(3分)
(2)解:可得 ![]() ,
, ![]() ,
,
![]() ,
,
= ![]() ,
, ![]() ,
,
∴y与x的回归模型为: ![]() .
.
(3)解:把2016年的年份代码x=6代入回归模型得 ![]() (百万件),
(百万件),
∴预计该市2016年的快递业务总量约为121.6百万件.
【解析】(1)根据表中所给的数据,得到点的坐标,在平面直角坐标系中画出散点图;(2)先求出年份代码x和快递量y的平均数,得到这组数据的样本中心点,利用最小二乘法求出线性回归方程的系数,代入样本中心点求出a的值,写出线性回归方程;(3)先求得2016年对于的年份代码,代入线性回归方程,即可求得该市2016年的快递业务总量.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
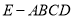 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.(1)求
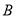 到平面
到平面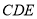 的距离
的距离(2)在线段
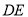 上是否存在一点
上是否存在一点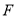 ,使
,使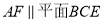 ?若存在,求出
?若存在,求出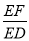 的值;若不存在,说明理由.
的值;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个命题:
①函数y=|x|与函数y=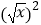 表示同一个函数;
表示同一个函数;
②奇函数的图象一定通过直角坐标系的原点;
③函数y=3(x﹣1)2的图象可由y=3x2的图象向右平移1个单位得到;
④若函数f(x)的定义域为[0,2],则函数f(2x)的定义域为[0,4];
⑤设函数f(x)是在区间[a.b]上图象连续的函数,且f(a)f(b)<0,则方程f(x)=0在区间[a,b]上至少有一实根.
其中正确命题的序号是 . (填上所有正确命题的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
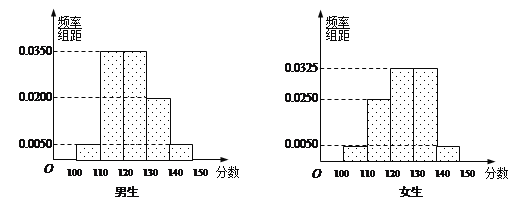
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
附:
P(K2≥k0)
0.100
0.050
0.010
0.001
k0
2.706
3.841
6.635
10.828
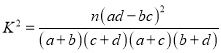 ,
, -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=lnx﹣
 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A.(1,2)
B.(2,3)
C.(e,3)
D.(e,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知﹣3≤log
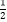 x≤﹣
x≤﹣  ,求函数f(x)=log2
,求函数f(x)=log2  log2
log2  的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC.
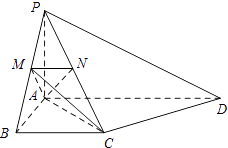
(1)证明:平面AMN⊥平面PBA;
(2)若M为PB的中点,求二面角M﹣AC﹣D的余弦值.
相关试题

