【题目】如图,PA⊥平面ABCD,AB⊥AD,AD∥BC,PA=AB=BC,AD=2AB,点M,N分别在PB,PC上,且MN∥BC. 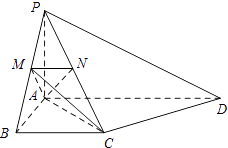
(1)证明:平面AMN⊥平面PBA;
(2)若M为PB的中点,求二面角M﹣AC﹣D的余弦值.
参考答案:
【答案】
(1)证明:∵MN∥BC,BC∥AD,∴MN∥AD,
∵PA⊥平面ABCD,
∴PA⊥AD,
又∵AD⊥AB,PA∩AB=A,
∴AD⊥平面PBA,
∴MN⊥平面PBA,
又∵MN平面AMN,
∴平面AMN⊥平面PBA.
(2)解:如图,以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系A﹣xyz,
不妨设AB=1,则:A(0,0,0),C(1,1,0), ![]() ,
,
∴ ![]() ,
, ![]() ,
,
设平面AMC的法向量 ![]() ,则:
,则: 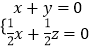 ,
,
令x=1,则y=﹣1,z=﹣1,∴ ![]()
平面ADC的一个法向量为 ![]() ,
,
∴ 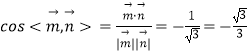 ,
,
∴二面角M﹣AC﹣D的余弦值为 ![]() .
.
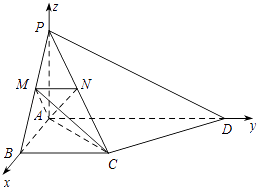
【解析】(1)推导出MN∥AD,PA⊥AD,从而AD⊥平面PBA,进而MN⊥平面PBA,由此能证明平面AMN⊥平面PBA.(2)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系A﹣xyz,利用向量法能求出二面角M﹣AC﹣D的余弦值.
【考点精析】本题主要考查了平面与平面垂直的判定的相关知识点,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如表中给出了2011年~2015年某市快递业务总量的统计数据(单位:百万件)
年份
2011
2012
2013
2014
2015
年份代码
1
2
3
4
5
快递业务总量
34
55
71
85
105
(1)在图中画出所给数据的折线图;
(2)建立一个该市快递量y关于年份代码x的线性回归模型;
(3)利用(2)所得的模型,预测该市2016年的快递业务总量.
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:
斜率: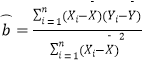 ,纵截距:
,纵截距: 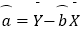 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=lnx﹣
 的零点所在的大致区间是( )
的零点所在的大致区间是( )
A.(1,2)
B.(2,3)
C.(e,3)
D.(e,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知﹣3≤log
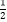 x≤﹣
x≤﹣  ,求函数f(x)=log2
,求函数f(x)=log2  log2
log2  的值域.
的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】
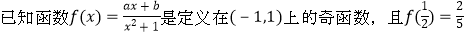 .
.
(1)确定函数f(x)的解析式;
(2)当x∈(﹣1,1)时判断函数f(x)的单调性,并证明;
(3)解不等式f(2x﹣1)+f(x)<0. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
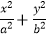 =1(a>b>0)的右焦点为F2(1,0),点P(1,
=1(a>b>0)的右焦点为F2(1,0),点P(1, 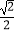 )在椭圆C上.
)在椭圆C上.
(1)求椭圆C的方程;
(2)过坐标原点O的两条直线EF,MN分别与椭圆C交于E,F,M,N四点,且直线OE,OM的斜率之积为﹣ ,求证:四边形EMFN的面积为定值.
,求证:四边形EMFN的面积为定值. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义在
 上的奇函数
上的奇函数 ,当
,当 时,
时,  ,则关于
,则关于 的函数
的函数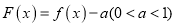 的所有零点之和为( )
的所有零点之和为( )A.
 B.
B.  C.
C.  D.
D. 
相关试题

