搜索
【题目】如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各面中，面积最大的是（ ）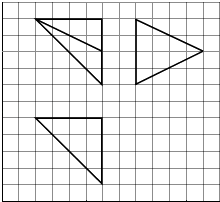 
A.8
B.
C.12
D.16
参考答案：
【答案】C
【解析】解：根据题意，得； 该几何体是如图所示的三棱锥A﹣BCD，
且该三棱锥是放在棱长为4的正方体中，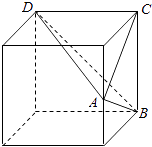
所以，在三棱锥A﹣BCD中，BD=4 
，AC=AB= 
= 
，AD= 
=6，
S△ABC= 
×4×4=8．S△ADC= × 
=4 
，S△DBC= ×4×4=8，在三角形ABC中，作CE⊥ 
E，连结DE，则CE= 
= 
，DE= 
= 
，
S△ABD= 
=12．
故选：C．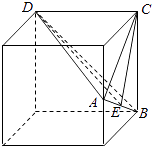
根据三视图得出该几何体是在棱长为4的正方体中的三棱锥，画出图形，求出各个面积即可．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知向量
=（2cos2x， 
）， 
=（1，sin2x），函数f（x）= ﹣1．
（1）当x=
时，求|a﹣b|的值；
（2）求函数f（x）的最小正周期以及单调递增区间；
（3）求方程f（x）=k，（0＜k＜2），在[﹣
， 
]内的所有实数根之和． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示的几何体中，四边形AA1B1B是边长为3的正方形，CC1=2，CC1∥AA1 ， 这个几何体是棱柱吗？若是，指出是几棱柱．若不是棱柱，请你试用一个平面截去一部分，使剩余部分是一个棱长为2的三棱柱，并指出截去的几何体的特征，在立体图中画出截面．
-
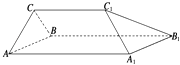
科目： 来源： 题型：
查看答案和解析>>【题目】正三棱柱ABC﹣A1B1C1的棱长都为2，E，F，G为 AB，AA1 ， A1C1的中点，则B1F 与面GEF成角的正弦值（ ）
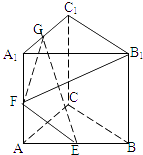
A.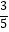
B.
C.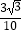
D.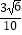
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，记长方体ABCD﹣A1B1C1D1被平行于棱B1C1的平面EFGH截去右上部分后剩下的几何体为Ω，则下列结论中不正确的是（ ）
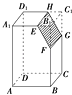
A.EH∥FG
B.四边形EFGH是平行四边形
C.Ω是棱柱
D.Ω是棱台 -
科目： 来源： 题型：
查看答案和解析>>【题目】在四棱锥
中，底面
为平行四边形， 
， 
， 
， 
点在底面
内的射影
在线段
上，且
， 
， 
为
的中点， 
在线段
上，且
.
（1）当
时，证明：平面
平面
；（2）当
时，求平面
与平面
所成的二面角的正弦值及四棱锥
的体积. -
科目： 来源： 题型：
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中，B1C与对角面DD1B1B所成角的大小是（ ）
A.15°
B.30°
C.45°
D.60°
相关试题
