【题目】在正方体ABCD﹣A1B1C1D1中,B1C与对角面DD1B1B所成角的大小是( )
A.15°
B.30°
C.45°
D.60°
参考答案:
【答案】B
【解析】解:以D点为坐标原点,以DA、DC、DD1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,
则A(2,0,0),B(2,2,0),C(0,2,0),C1(0,2,2)
∴ ![]() =(﹣2,0,2),
=(﹣2,0,2), ![]() =(﹣2,2,0),且
=(﹣2,2,0),且 ![]() 为平面BB1D1D的一个法向量.
为平面BB1D1D的一个法向量.
∴cos< ![]() ,
, ![]() >=
>= ![]() =
= ![]() ,
,
∴BC1与平面BB1D1D所成角的正弦值为 ![]() ,
,
∴BC1与平面BB1D1D所成角为30°.
故选:B.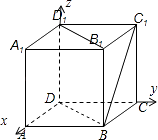
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则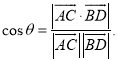 才能正确解答此题.
才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
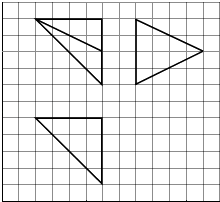
A.8
B.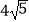
C.12
D.16 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,记长方体ABCD﹣A1B1C1D1被平行于棱B1C1的平面EFGH截去右上部分后剩下的几何体为Ω,则下列结论中不正确的是( )
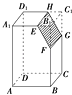
A.EH∥FG
B.四边形EFGH是平行四边形
C.Ω是棱柱
D.Ω是棱台 -
科目: 来源: 题型:
查看答案和解析>>【题目】在四棱锥
 中,底面
中,底面 为平行四边形,
为平行四边形,  ,
,  ,
,  ,
,  点在底面
点在底面 内的射影
内的射影 在线段
在线段 上,且
上,且 ,
,  ,
,  为
为 的中点,
的中点,  在线段
在线段 上,且
上,且 .
.
(1)当
 时,证明:平面
时,证明:平面 平面
平面 ;
;(2)当
 时,求平面
时,求平面 与平面
与平面 所成的二面角的正弦值及四棱锥
所成的二面角的正弦值及四棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
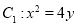 的焦点
的焦点 也是椭圆
也是椭圆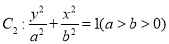 的一个焦点,
的一个焦点,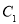 与
与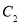 的公共弦的长为
的公共弦的长为 .
.(1)求
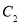 的方程;
的方程;(2)过点
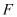 的直线
的直线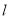 与
与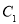 相交于
相交于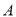 ,
,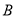 两点,与
两点,与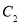 相交于
相交于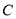 ,
,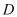 两点,且
两点,且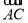 与
与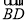 同向
同向(ⅰ)若
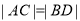 ,求直线
,求直线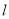 的斜率
的斜率(ⅱ)设
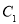 在点
在点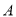 处的切线与
处的切线与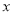 轴的交点为
轴的交点为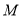 ,证明:直线
,证明:直线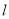 绕点
绕点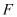 旋转时,
旋转时, 总是钝角三角形
总是钝角三角形 -
科目: 来源: 题型:
查看答案和解析>>【题目】一个透明密闭的正方体容器中,恰好盛有该容器一半容积的水,任意转动这个正方体,则水面在容器中的形状可以是:
①三角形;②矩形;③正方形;④正六边形.
其中正确的结论是(把你认为正确的序号都填上) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直三棱柱ABC﹣A1B1C1中,D为AC的中点,∠ABC=90°,AA1=AB=2,BC=3.
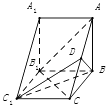
(1)求证:AB1∥平面BC1D;
(2)求三棱锥D﹣BC1C的体积.
相关试题

