【题目】已知向量 ![]() =(2cos2x,
=(2cos2x, ![]() ),
), ![]() =(1,sin2x),函数f(x)=
=(1,sin2x),函数f(x)= ![]()
![]() ﹣1.
﹣1.
(1)当x= ![]() 时,求|a﹣b|的值;
时,求|a﹣b|的值;
(2)求函数f(x)的最小正周期以及单调递增区间;
(3)求方程f(x)=k,(0<k<2),在[﹣ ![]() ,
, ![]() ]内的所有实数根之和.
]内的所有实数根之和.
参考答案:
【答案】
(1)
解:由向量 ![]() =(2cos2x,
=(2cos2x, ![]() ),
), ![]() =(1,sin2x),
=(1,sin2x),
则:a﹣b=(2cos2x﹣1, ![]() sin2x)
sin2x)
当x= ![]() 时,a﹣b=(2cos2
时,a﹣b=(2cos2 ![]() ﹣1,
﹣1, ![]() sin2×
sin2× ![]() )
)
=(0, ![]() )
)
那么:|a﹣b|= ![]()
(2)
解:f(x)=ab﹣1=1×2cos2x+ ![]() sin2x
sin2x
= ![]()
=1+cos2x+ ![]() sin2x﹣1
sin2x﹣1
=2sin(2x+ ![]() )
)
∴最小正周期T= ![]()
由sinx的图象和性质,可知x ![]() ,(k∈Z)是增区间.
,(k∈Z)是增区间.
∴2x+ ![]()
![]() 是增区间,即:
是增区间,即: ![]() ,(k∈Z)
,(k∈Z)
解得: ![]() ,(k∈Z)
,(k∈Z)
所以,f(x)的单调增区间为: ![]() ,(k∈Z)
,(k∈Z)
(3)
解:由方程f(x)=k,(0<k<2),得 ![]() .
.
∵ ![]() 的周期T=π,又
的周期T=π,又 ![]() ,
,
∴ ![]() 在
在 ![]() 内有2个周期.
内有2个周期.
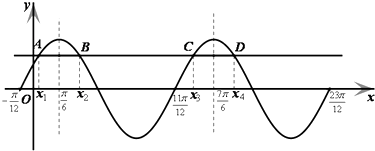
∵ ![]() ,∴方程
,∴方程 ![]() 在
在 ![]() 内有4个交点,即有4个实根.
内有4个交点,即有4个实根.
根据图象的对称性,有 ![]() ,
, ![]() ,
,
∴所有实数根之和=x1+x2+x3+x4+x5+x6= ![]() .
.
【解析】(1)根据平面向量加减的运算法则求出a﹣b,化简,将x= ![]() 带入,求模长.(2)根据平面向量乘积的运算法则求出f(x),将其化简,结合三角函数的图象和性质即可得到答案.(3)利用三角函数的图象和性质,在[﹣
带入,求模长.(2)根据平面向量乘积的运算法则求出f(x),将其化简,结合三角函数的图象和性质即可得到答案.(3)利用三角函数的图象和性质,在[﹣ ![]() ,
, ![]() ]内求出方程f(x)=k时,x的值,即可解决问题.
]内求出方程f(x)=k时,x的值,即可解决问题.
-
科目: 来源: 题型:
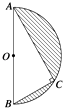
查看答案和解析>>【题目】如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积(其中∠BAC=30°)及其体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学用“五点法”画函数f(x)=Asin(ωx+φ)(ω>0,|φ|<
 )在某一个周期内的图象时,列表并填入的部分数据如表:
)在某一个周期内的图象时,列表并填入的部分数据如表: x

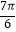
ωx+φ
0

π
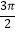
2π
Asin(ωx+φ)
0
2
0
﹣2
(1)请将上表数据补全,并直接写出函数f(x)的解析式;
(2)当x∈[0, ]时,求函数f(x)的值域.
]时,求函数f(x)的值域. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知单位圆O上的两点A,B及单位圆所在平面上的一点P,满足
 =m
=m  +
+  (m为常数).
(m为常数). 
(1)如图,若四边形OABP为平行四边形,求m的值;
(2)若m=2,求| |的取值范围.
|的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的几何体中,四边形AA1B1B是边长为3的正方形,CC1=2,CC1∥AA1 , 这个几何体是棱柱吗?若是,指出是几棱柱.若不是棱柱,请你试用一个平面截去一部分,使剩余部分是一个棱长为2的三棱柱,并指出截去的几何体的特征,在立体图中画出截面.
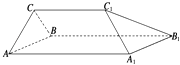
-
科目: 来源: 题型:
查看答案和解析>>【题目】正三棱柱ABC﹣A1B1C1的棱长都为2,E,F,G为 AB,AA1 , A1C1的中点,则B1F 与面GEF成角的正弦值( )
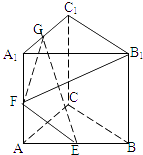
A.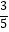
B.
C.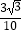
D.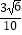
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面中,面积最大的是( )
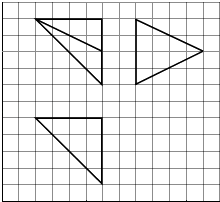
A.8
B.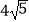
C.12
D.16
相关试题

