【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() (
(![]() 为参数),将
为参数),将![]() 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的![]() 和
和![]() 倍后得到曲线
倍后得到曲线![]() .以平面直角坐标系
.以平面直角坐标系![]() 的原点
的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)试写出曲线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的参数方程;
的参数方程;
(2)在曲线![]() 上求一点
上求一点![]() ,使点
,使点![]() 到直线
到直线![]() 的距离最小,并求此最小值.
的距离最小,并求此最小值.
参考答案:
【答案】(1)![]() ,
,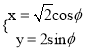 (
(![]() 为参数);(2)
为参数);(2)![]() .
.
【解析】试题分析:(1)根据![]() 将曲线
将曲线![]() 的参数方程化为普通方程:
的参数方程化为普通方程: ![]() ,再根据
,再根据![]() 将直角坐标方程化为极坐标方程
将直角坐标方程化为极坐标方程![]() ;由图像变换可得曲线
;由图像变换可得曲线![]() 的参数方程是
的参数方程是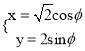 (2)先根据
(2)先根据![]() 将直线
将直线![]() 化为直角坐标方程
化为直角坐标方程![]() ,再根据点到直线距离公式得
,再根据点到直线距离公式得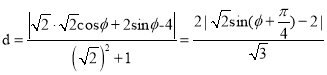 ,利用三角函数有界性确定函数最小值,并确定取最小值时
,利用三角函数有界性确定函数最小值,并确定取最小值时![]() 的值,进而确定点
的值,进而确定点![]() 坐标.
坐标.
试题解析:(1)由已知得曲线![]() 的直角坐标方程是
的直角坐标方程是![]() ,
,
所以曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
根据已知曲线![]() 的参数方程
的参数方程![]() 伸缩变换得到曲线
伸缩变换得到曲线![]() 的参数方程是
的参数方程是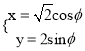 (
(![]() 为参数).
为参数).
(2)设![]() ,由已知得直线
,由已知得直线![]() 的直角坐标方程是
的直角坐标方程是![]() ,
,
即![]() ,所以点
,所以点![]() 到直线
到直线![]() 的距离
的距离
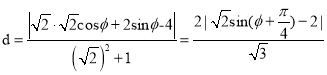 ,
,
当![]() 即
即![]() 时,
时, 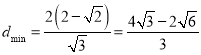 ,此时点
,此时点![]() 的坐标是
的坐标是![]() ,
,
所以曲线![]() 上的一点
上的一点![]()
![]() 到直线
到直线![]() 的距离最小,最小值是
的距离最小,最小值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为椭圆
为椭圆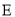 的左右焦点,点
的左右焦点,点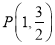 为其上一点,且有
为其上一点,且有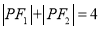 .
.(1)求椭圆
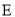 的标准方程;
的标准方程;(2)过
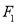 的直线
的直线 与椭圆
与椭圆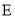 交于
交于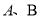 两点,过
两点,过 与
与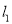 平行的直线
平行的直线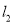 与椭圆
与椭圆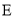 交于
交于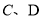 两点,求四边形
两点,求四边形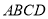 的面积
的面积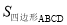 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,
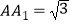 .M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.
.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点. 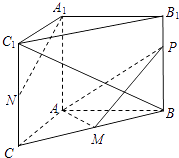
(1)求证:平面APM⊥平面BB1C1C;
(2)若P为线段BB1的中点,求证:A1N∥平面APM;
(3)试判断直线BC1与平面APM是否能够垂直.若能垂直,求PB的值;若不能垂直,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知空间四边形
 ,
,  分别在
分别在 上,
上,(1) 若
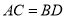 ,异面直线
,异面直线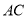 与
与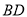 所成的角的大小为
所成的角的大小为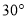 ,求
,求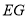 和
和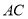 所成的角的大小;
所成的角的大小;(2)当四边形
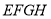 是平面四边形时,试判断
是平面四边形时,试判断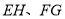 与
与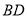 三条直线的位置关系,并选择其中一种位置关系说明理由;
三条直线的位置关系,并选择其中一种位置关系说明理由;(3)已知当
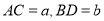 ,异面直线
,异面直线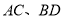 所成角为
所成角为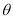 ,当四边形
,当四边形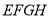 是平行四边形时,试判断
是平行四边形时,试判断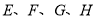 点在什么位置时,四边形
点在什么位置时,四边形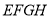 的面积最大,试求出最大面积并说明理由。
的面积最大,试求出最大面积并说明理由。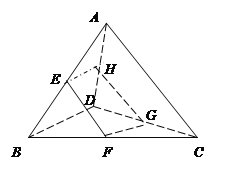
-
科目: 来源: 题型:
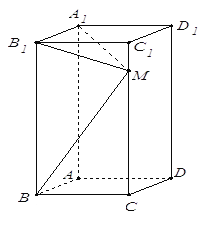
查看答案和解析>>【题目】如图所示,在长方体
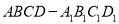 中,
中,  ,
, 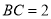 ,
, 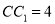 ,
, 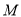 为棱
为棱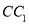 上一点,
上一点,(1)若
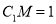 ,求异面直线
,求异面直线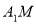 和
和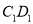 所成角的正切值;
所成角的正切值;(2)若
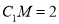 ,求证
,求证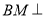 平面
平面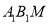 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
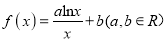 的图像在点
的图像在点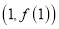 处的切线方程为
处的切线方程为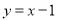 .
.(1)求实数
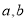 的值及函数
的值及函数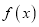 的单调区间;
的单调区间;(2)当
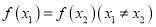 时,比较
时,比较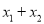 与
与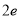 (
(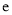 为自然对数的底数)的大小.
为自然对数的底数)的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}满足:a1=1,a2=2,且an+1=2an+3an﹣1(n≥2,n∈N+).
(1)设bn=an+1+an(n∈N+),求证{bn}是等比数列;
(2)(i)求数列{an}的通项公式;
(ii)求证:对于任意n∈N+都有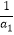 +
+ 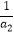 +…+
+…+ 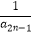 +
+ 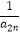 <
<  成立.
成立.
相关试题

