【题目】已知空间四边形![]() ,
, ![]() 分别在
分别在![]() 上,
上,
(1) 若![]() ,异面直线
,异面直线![]() 与
与![]() 所成的角的大小为
所成的角的大小为![]() ,求
,求![]() 和
和![]() 所成的角的大小;
所成的角的大小;
(2)当四边形![]() 是平面四边形时,试判断
是平面四边形时,试判断![]() 与
与![]() 三条直线的位置关系,并选择其中一种位置关系说明理由;
三条直线的位置关系,并选择其中一种位置关系说明理由;
(3)已知当![]() ,异面直线
,异面直线![]() 所成角为
所成角为![]() ,当四边形
,当四边形![]() 是平行四边形时,试判断
是平行四边形时,试判断![]() 点在什么位置时,四边形
点在什么位置时,四边形![]() 的面积最大,试求出最大面积并说明理由。
的面积最大,试求出最大面积并说明理由。
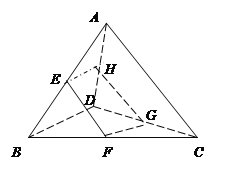
参考答案:
【答案】(1)![]() 或
或![]() (2)
(2)![]() 或者
或者![]() 相交,(3)
相交,(3)![]() 分别为
分别为![]() 中点时,四边形
中点时,四边形![]() 的面积最大,
的面积最大, ![]()
【解析】试题分析:(1)根据题意可得四边形![]() 为菱形,而菱形对角线平分对角可得
为菱形,而菱形对角线平分对角可得![]() 和
和![]() 所成的角大小(2)先定位置:
所成的角大小(2)先定位置: ![]() 或者
或者![]() 相交,再分情况证明:当
相交,再分情况证明:当![]() 时,利用线面平行性质与判定定理可得
时,利用线面平行性质与判定定理可得 ![]() ;当
;当![]() 相交时,可得
相交时,可得![]() 相交(3)先根据线线角得四边形
相交(3)先根据线线角得四边形![]() 一内角为
一内角为![]() ,利用平行四边形面积公式可得
,利用平行四边形面积公式可得![]() ,再根据相似比得
,再根据相似比得![]() ,最后根据基本不等式求最值
,最后根据基本不等式求最值
试题解析:解:(1)![]() 或
或![]()
(2)![]() 共面
共面![]() 或者
或者![]() 相交,设交点为
相交,设交点为![]()
(以下理由只要求写出一种即对)
![]() 时
时
![]() 且
且![]()
又![]() 且
且![]()
![]()
即三条直线互相平行
![]() 时
时
![]()
![]()
又![]()
![]()
又![]()
![]() 即三条直线交于一点
即三条直线交于一点
(3) ![]()
在![]() 中,
中, ![]() ,在
,在![]() 中,
中, ![]()
![]()
![]()
![]() 时
时![]() 取得最大值,即
取得最大值,即![]() 分别为
分别为![]() 中点时,四边形
中点时,四边形![]() 的面积最大,
的面积最大, ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市对贫困家庭自主创业给予小额贷款补贴,每户贷款额为
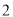 万元,贷款期限有
万元,贷款期限有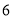 个月、
个月、 个月、
个月、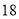 个月、
个月、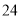 个月、
个月、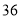 个月五种,这五种贷款期限政府分别需要补助
个月五种,这五种贷款期限政府分别需要补助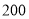 元、
元、 元、
元、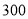 元、
元、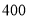 元、
元、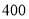 元,从
元,从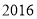 年享受此项政策的困难户中抽取了
年享受此项政策的困难户中抽取了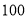 户进行了调查统计,选取贷款期限的频数如下表:
户进行了调查统计,选取贷款期限的频数如下表:贷款期限
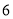 个月
个月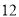 个月
个月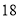 个月
个月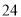 个月
个月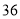 个月
个月频数
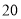
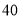
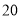

以商标各种贷款期限的频率作为
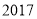 年贫困家庭选择各种贷款期限的概率.
年贫困家庭选择各种贷款期限的概率.(1)某小区
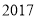 年共有
年共有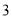 户准备享受此项政策,计算其中恰有两户选择贷款期限为
户准备享受此项政策,计算其中恰有两户选择贷款期限为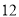 个月的概率;
个月的概率;(2)设给享受此项政策的某困难户补贴为
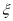 元,写出
元,写出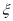 的分布列,若预计
的分布列,若预计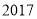 年全市有
年全市有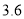 万户享受此项政策,估计
万户享受此项政策,估计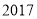 年该市共要补贴多少万元.
年该市共要补贴多少万元. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为椭圆
为椭圆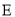 的左右焦点,点
的左右焦点,点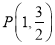 为其上一点,且有
为其上一点,且有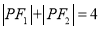 .
.(1)求椭圆
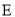 的标准方程;
的标准方程;(2)过
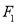 的直线
的直线 与椭圆
与椭圆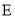 交于
交于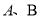 两点,过
两点,过 与
与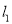 平行的直线
平行的直线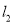 与椭圆
与椭圆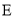 交于
交于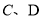 两点,求四边形
两点,求四边形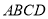 的面积
的面积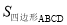 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,∠BAC=90°,AB=AC=2,
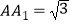 .M,N分别为BC和CC1的中点,P为侧棱BB1上的动点.
.M,N分别为BC和CC1的中点,P为侧棱BB1上的动点. 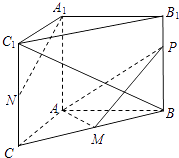
(1)求证:平面APM⊥平面BB1C1C;
(2)若P为线段BB1的中点,求证:A1N∥平面APM;
(3)试判断直线BC1与平面APM是否能够垂直.若能垂直,求PB的值;若不能垂直,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
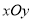 中,已知曲线
中,已知曲线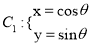 (
(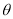 为参数),将
为参数),将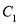 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的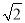 和
和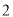 倍后得到曲线
倍后得到曲线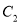 .以平面直角坐标系
.以平面直角坐标系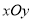 的原点
的原点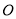 为极点,
为极点, 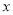 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线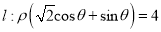 .
.(1)试写出曲线
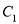 的极坐标方程与曲线
的极坐标方程与曲线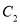 的参数方程;
的参数方程;(2)在曲线
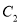 上求一点
上求一点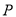 ,使点
,使点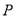 到直线
到直线 的距离最小,并求此最小值.
的距离最小,并求此最小值. -
科目: 来源: 题型:
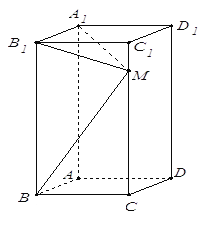
查看答案和解析>>【题目】如图所示,在长方体
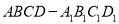 中,
中,  ,
, 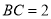 ,
, 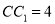 ,
, 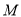 为棱
为棱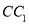 上一点,
上一点,(1)若
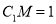 ,求异面直线
,求异面直线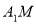 和
和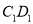 所成角的正切值;
所成角的正切值;(2)若
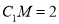 ,求证
,求证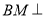 平面
平面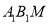 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
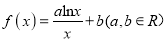 的图像在点
的图像在点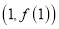 处的切线方程为
处的切线方程为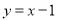 .
.(1)求实数
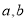 的值及函数
的值及函数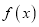 的单调区间;
的单调区间;(2)当
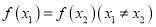 时,比较
时,比较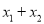 与
与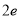 (
(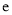 为自然对数的底数)的大小.
为自然对数的底数)的大小.
相关试题

