【题目】(本小题满分14分)
在四棱锥P-ABCD中,BC∥AD,PA⊥PD,AD=2BC,AB=PB, E为PA的中点.
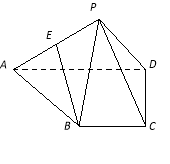
(1)求证:BE∥平面PCD;
(2)求证:平面PAB⊥平面PCD.
参考答案:
【答案】证明见解析.
【解析】
试题分析:(1)要证明BE∥平面PCD,就是要在平面PCD上找到一条与BE平行的直线,由判定定理,从已知![]() ,
,![]() 又是
又是![]() 中点,因此我们取
中点,因此我们取![]() 中点
中点![]() ,可得
,可得![]() ,且
,且![]() ,从而有
,从而有![]() 且
且![]() ,于是
,于是![]() 是平行四边形,
是平行四边形,![]() ,平行线找到了;(2)要证明平面PAB⊥平面PCD,而题中已知PA⊥PD,由面面垂直的性质,
,平行线找到了;(2)要证明平面PAB⊥平面PCD,而题中已知PA⊥PD,由面面垂直的性质,![]() 中一定有一条直线与其中一个平面垂直,由已知
中一定有一条直线与其中一个平面垂直,由已知![]() ,因此
,因此![]() ,再由(1)
,再由(1)![]() ,这样结合
,这样结合![]() 就有
就有![]() ,于是有面面垂直.
,于是有面面垂直.
试题解析:(1)取PD的中点F,连接EF,CF.
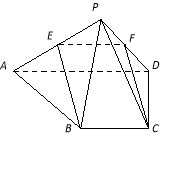
因为E为PA的中点,所以EF∥AD,EF=AD.
因为BC∥AD,BC=AD,
所以EF∥BC,EF=BC.
所以四边形BCFE为平行四边形.
所以BE∥CF. 4分
因为BE平面PCD,CF平面PCD,
所以BE∥平面PCD. 6分
(2)因为AB=PB,E为PA的中点,所以PA⊥BE.
因为BE∥CF,所以PA⊥CF. 9分
因为PA⊥PD,PD平面PCD,CF平面PCD,PD∩CF=F,
所以PA⊥平面PCD. 12分
因为PA平面PAB,所以平面PAB平面PCD. 14分
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产一批
 产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批
产品需要原材料500吨,每吨原材料可创造利润12万元,该公司通过设备升级,生产这批 产品所需原材料减少了
产品所需原材料减少了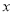 吨,且每吨原材料创造的利润提高
吨,且每吨原材料创造的利润提高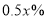 ;若将少用的
;若将少用的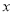 吨原材料全部用于生产公司新开发的
吨原材料全部用于生产公司新开发的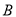 产品,每吨原材料创造的利润为
产品,每吨原材料创造的利润为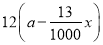 万元
万元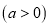 .
.(1)若设备升级后生产这批
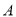 产品的利润不低于原来生产该批
产品的利润不低于原来生产该批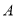 产品的利润,求
产品的利润,求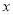 的取值范围;
的取值范围;(2)若生产这批
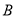 产品的利润始终不高于设备升级后生产这批
产品的利润始终不高于设备升级后生产这批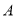 产品的利润,求
产品的利润,求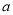 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从高二年级学生中随机抽取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
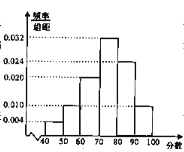
(1)若该校高二年级共有学生1000人,试估计成绩不低于60分的人数;
(2)求该校高二年级全体学生期中考试成绩的众数、中位数和平均数的估计值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方体
 的棱长为1,
的棱长为1, 分别是棱
分别是棱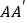 ,
, 的中点,过直线
的中点,过直线 的平面分别与棱
的平面分别与棱 、
、 交于
交于 ,设
,设 ,
, ,给出以下四个命题:
,给出以下四个命题:①四边形
 为平行四边形;
为平行四边形;②若四边形
 面积
面积 ,
, ,则
,则 有最小值;
有最小值;③若四棱锥
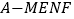 的体积
的体积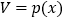
 ,
, ,则
,则 为常函数;
为常函数;④若多面体
 的体积
的体积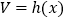 ,
, ,则
,则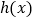 为单调函数.
为单调函数.其中假命题为( )
A. ① ③ B. ② C. ③④ D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地参加2015 年夏令营的
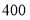 名学生的身体健康情况,将学生编号为
名学生的身体健康情况,将学生编号为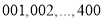 ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为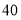 的样本,且抽到的最小号码为
的样本,且抽到的最小号码为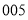 ,已知这
,已知这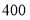 名学生分住在三个营区,从
名学生分住在三个营区,从 到
到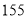 在第一营区,从
在第一营区,从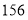 到
到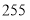 在第二营区,从
在第二营区,从 到
到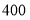 在第三营区,则第一、第二、第三营区被抽中的人数分别为( )
在第三营区,则第一、第二、第三营区被抽中的人数分别为( )A.
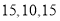 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
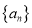 是首项为0的递增数列,
是首项为0的递增数列,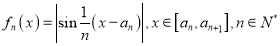 ,满足:对于任意的
,满足:对于任意的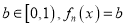 总有两个不同的根,则
总有两个不同的根,则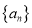 的通项公式为_________
的通项公式为_________ -
科目: 来源: 题型:
查看答案和解析>>【题目】口袋中装有质地大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸一个球,记下编号,放回后乙再摸一个球,记下编号.如果两个编号的和为偶数就算甲胜,否则算乙胜.
(1)求甲胜且编号的和为6的事件发生的概率;
(2)这种游戏规则公平吗?说明理由.
相关试题

