【题目】口袋中装有质地大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸一个球,记下编号,放回后乙再摸一个球,记下编号.如果两个编号的和为偶数就算甲胜,否则算乙胜.
(1)求甲胜且编号的和为6的事件发生的概率;
(2)这种游戏规则公平吗?说明理由.
参考答案:
【答案】(1)![]() ;(2)游戏规则不公平,理由见解析.
;(2)游戏规则不公平,理由见解析.
【解析】
试题分析:(1)相当于两人掷含有![]() 个面的色子,共
个面的色子,共![]() 种情况,然后输入和为偶数,且和为
种情况,然后输入和为偶数,且和为![]() 的情况种数,然后用古典概型求概率;(2)偶数,就是甲胜,其他情况乙胜,分别算出甲胜的概率和乙胜的概率,比较是否相等,相等就公平,不相等就不公平.
的情况种数,然后用古典概型求概率;(2)偶数,就是甲胜,其他情况乙胜,分别算出甲胜的概率和乙胜的概率,比较是否相等,相等就公平,不相等就不公平.
试题解析:解:(1)设“甲胜且编号的和为6”为事件![]() .
.
甲编号为![]() ,乙编号为
,乙编号为![]() ,
,![]() 表示一个基本事件,
表示一个基本事件,
则两人摸球结果包括(1,2),(1,3),…,(1,5),(2,1),(2,2),…,(5,4),(5,5)共25个基本事件;
![]() 包括的基本事件有(1,5),(2,4),(3,3),(4,2),(5,1)共5个.
包括的基本事件有(1,5),(2,4),(3,3),(4,2),(5,1)共5个.
∴![]() .
.
答:甲胜且编号的和为6的事件发生的概率为![]() .
.
(2)这种游戏不公平.
设“甲胜”为事件![]() ,“乙胜”为事件
,“乙胜”为事件![]() .甲胜即两个编号的和为偶数所包含基本事件数为以下13个:(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(5,5).
.甲胜即两个编号的和为偶数所包含基本事件数为以下13个:(1,1),(1,3),(1,5),(2,2),(2,4),(3,1),(3,3),(3,5),(4,2),(4,4),(5,1),(5,3),(5,5).
所以甲胜的概率为![]() ,乙胜的概率为
,乙胜的概率为![]() ,
,
∵![]() ,∴这种游戏规则不公平.
,∴这种游戏规则不公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分14分)
在四棱锥P-ABCD中,BC∥AD,PA⊥PD,AD=2BC,AB=PB, E为PA的中点.
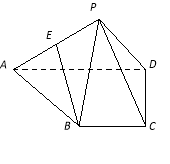
(1)求证:BE∥平面PCD;
(2)求证:平面PAB⊥平面PCD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某地参加2015 年夏令营的
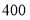 名学生的身体健康情况,将学生编号为
名学生的身体健康情况,将学生编号为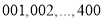 ,采用系统抽样的方法抽取一个容量为
,采用系统抽样的方法抽取一个容量为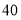 的样本,且抽到的最小号码为
的样本,且抽到的最小号码为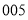 ,已知这
,已知这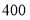 名学生分住在三个营区,从
名学生分住在三个营区,从 到
到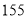 在第一营区,从
在第一营区,从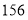 到
到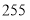 在第二营区,从
在第二营区,从 到
到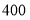 在第三营区,则第一、第二、第三营区被抽中的人数分别为( )
在第三营区,则第一、第二、第三营区被抽中的人数分别为( )A.
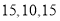 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设数列
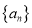 是首项为0的递增数列,
是首项为0的递增数列,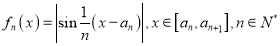 ,满足:对于任意的
,满足:对于任意的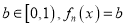 总有两个不同的根,则
总有两个不同的根,则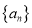 的通项公式为_________
的通项公式为_________ -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知圆
中,已知圆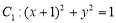 ,圆
,圆 .
.(1)若过点
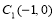 的直线
的直线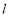 被圆
被圆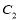 截得的弦长为
截得的弦长为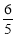 ,求直线
,求直线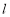 的方程;
的方程;(2)圆
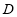 是以1为半径,圆心在圆
是以1为半径,圆心在圆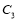 :
: 上移动的动圆 ,若圆
上移动的动圆 ,若圆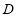 上任意一点
上任意一点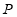 分别作圆
分别作圆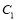 的两条切线
的两条切线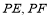 ,切点为
,切点为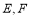 ,求
,求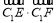 的取值范围;
的取值范围;(3)若动圆
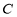 同时平分圆
同时平分圆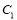 的周长、圆
的周长、圆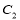 的周长,则动圆
的周长,则动圆 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.
是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1.
(1)求数列{bn}的通项公式;
(2)令cn=
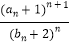 ,Tn是数列{cn}的前n项和,求证:
,Tn是数列{cn}的前n项和,求证: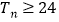
-
科目: 来源: 题型:
查看答案和解析>>【题目】某城市
 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以 ,
, ,
, ,
, ,
, ,
, ,
, 分组的频率分布直方图如图.
分组的频率分布直方图如图.
(I)求直方图中
 的值;
的值; (II)求月平均用电量的众数和中位数;
(III)在月平均用电量为
 ,
, ,
, ,
, 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取 户居民,则月平均用电量在
户居民,则月平均用电量在 的用户中应抽取多少户?
的用户中应抽取多少户?
相关试题

