【题目】如图,四棱锥![]() 的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=
的底面为菱形 且∠ABC=120°,PA⊥底面ABCD,AB=2,PA=![]() ,
,
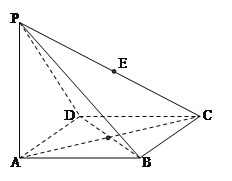
(1)求证:平面PBD⊥平面PAC;
(2)求三棱锥P--BDC的体积。
(3)在线段PC上是否存在一点E,使PC⊥平面EBD成立.如果存在,求出EC的长;如果不存在,请说明理由。
参考答案:
【答案】(1)见解析;(2)1;(3)![]() .
.
【解析】试题分析:
(1)要证面面垂直,一般先证线面垂直,也即要证线线垂直,由菱形可得![]() ,又由
,又由![]() 平面
平面![]() 得
得![]() ,从而可得直线与平面
,从而可得直线与平面![]() 垂直,从而得证面面垂直;
垂直,从而得证面面垂直;
(2)三棱锥![]() 的底面是
的底面是![]() ,高为
,高为![]() ,由体积公式可得体积;
,由体积公式可得体积;
(3)假设存在,由线面垂直可得线线垂直,设![]() ,则
,则![]() ,在
,在![]() 中由相似三角形可求得
中由相似三角形可求得![]() 长,反之只要有
长,反之只要有![]() ,就可得
,就可得![]() 平面
平面![]() .
.
试题解析:
(1) 略证:![]() 通过证BD⊥AC,BD⊥PA,得出BD⊥平面PAC,又BD在平面PBD内,所以平面PBD⊥平面PAD
通过证BD⊥AC,BD⊥PA,得出BD⊥平面PAC,又BD在平面PBD内,所以平面PBD⊥平面PAD
(2) ![]()
(3)假设存在,设![]() ,则
,则![]()
![]() ,Δ
,Δ![]() ∽ΔCPA ,
∽ΔCPA , ![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|(x-3)(x+a)<0,a∈R},集合B={x∈Z|x2-3x-4<0}.
(1)若A∩B的子集个数为4,求a的范围;
(2)若a∈Z,当A∩B≠
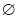 时,求a的最小值,并求当a取最小值时A∪B.
时,求a的最小值,并求当a取最小值时A∪B. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图①,正三角形
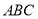 的边长为4,
的边长为4,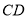 是
是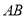 边上的高,
边上的高,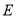 ,
,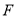 分别是
分别是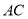 和
和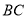 边的中点,现将△
边的中点,现将△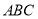 沿
沿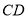 翻折成直二面角
翻折成直二面角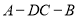 ,如图②.
,如图②.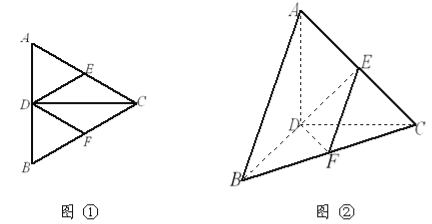
(1)判断直线
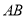 与平面
与平面 的位置关系,并说明理由;
的位置关系,并说明理由;(2)求棱锥
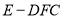 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段:
 ,
,  ,
,  ,…
,… 后得到如下频率分布直方图.
后得到如下频率分布直方图.
(1)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的平均分、众数、中位数;(小数点后保留一位有效数字)
(2)用分层抽样的方法在各分数段的学生中抽取一个容量为20的样本,则各分数段抽取的人数分别是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】设p:实数x满足
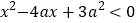 ,其中
,其中 ,命题
,命题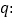 实数
实数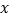 满足
满足|x-3|≤1 .
(1)若
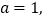 且
且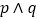 为真,求实数
为真,求实数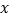 的取值范围;
的取值范围;(2)若
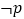 是
是
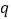 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
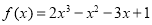 .若
.若 的一个零点附近的函数值如下所示,请用二分法求出方程
的一个零点附近的函数值如下所示,请用二分法求出方程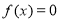 的一个正实数解的近似值(精确度0.1).
的一个正实数解的近似值(精确度0.1).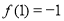 ,
,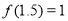 ,
,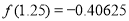 ,
,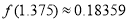 ,
,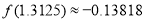 ,
,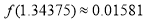 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】东亚运动会将于2013年10月6日在天津举行.为了搞好接待工作,组委会打算学习北京奥运会招募大量志愿者的经验,在某学院招募了16名男志愿者和14名女志愿者,调查发现,男女志愿者中分别有10人和6人喜爱运动,其余人不喜欢运动.
(1)根据以上数据完成以下2×2列联表:
喜爱运动
不喜爱运动
总计
男
10
16
女
6
14
总计
30
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有4人会外语),抽取2名负责翻译工作,那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少?
参考公式:K2=
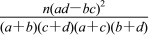 ,其中
,其中n=a+b+c+d.
参考数据:
P(K2≥k)
0.40
0.25
0.10
0.010
k
0.708
1.323
2.706
6.635
相关试题

