【题目】观察下列等式:
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2=
)﹣2= ![]() ×1×2;
×1×2;
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+sin(
)﹣2+sin( ![]() )﹣2=
)﹣2= ![]() ×2×3;
×2×3;
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+sin(
)﹣2+…+sin( ![]() )﹣2=
)﹣2= ![]() ×3×4;
×3×4;
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+sin(
)﹣2+…+sin( ![]() )﹣2=
)﹣2= ![]() ×4×5;
×4×5;
…
照此规律,
(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+(sin
)﹣2+…+(sin ![]() )﹣2= .
)﹣2= .
参考答案:
【答案】![]() n(n+1)
n(n+1)
【解析】解:观察下列等式:(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2=
)﹣2= ![]() ×1×2;(sin
×1×2;(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+sin(
)﹣2+sin( ![]() )﹣2=
)﹣2= ![]() ×2×3;(sin
×2×3;(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+sin(
)﹣2+…+sin( ![]() )﹣2=
)﹣2= ![]() ×3×4;(sin
×3×4;(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+sin(
)﹣2+…+sin( ![]() )﹣2=
)﹣2= ![]() ×4×5;
×4×5;
…
照此规律(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+(sin
)﹣2+(sin ![]() )﹣2+…+(sin
)﹣2+…+(sin ![]() )﹣2=
)﹣2= ![]() ×n(n+1),
×n(n+1),
故答案为: ![]() n(n+1)
n(n+1)
由题意可以直接得到答案.;本题考查了归纳推理的问题,关键是找到相对应的规律,属于基础题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T性质.下列函数中具有T性质的是( )
A.y=sinx
B.y=lnx
C.y=ex
D.y=x3 -
科目: 来源: 题型:
查看答案和解析>>【题目】漳州市博物馆为了保护一件珍贵文物,需要在馆内一种透明又密封的长方体玻璃保护罩内充入保护液体.该博物馆需要支付的总费用由两部分组成:①罩内该种液体的体积比保护罩的容积少0.5立方米,且每立方米液体费用500元;②需支付一定的保险费用,且支付的保险费用与保护罩容积成反比,当容积为2立方米时,支付的保险费用为4000元.
(Ⅰ)求该博物馆支付总费用
 与保护罩容积
与保护罩容积 之间的函数关系式;
之间的函数关系式;(Ⅱ)求该博物馆支付总费用的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥V﹣ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=
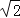 ,O,M分别为AB,VA的中点.
,O,M分别为AB,VA的中点.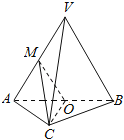
(1)求证:VB∥平面MOC;
(2)求证:平面MOC⊥平面VAB
(3)求三棱锥V﹣ABC的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
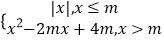 ,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是 .
,其中m>0,若存在实数b,使得关于x的方程f(x)=b有三个不同的根,则m的取值范围是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】随着互联网的发展,移动支付(又称手机支付)越来越普遍,某学校兴趣小组为了了解移动支付在大众中的熟知度,对15-65岁的人群随机抽样调查,调查的问题是“你会使用移动支付吗?”其中,回答“会”的共有
 个人,把这
个人,把这 个人按照年龄分成5组:第1组
个人按照年龄分成5组:第1组 ,第2组
,第2组 ,第3组
,第3组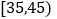 ,第4组
,第4组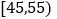 ,第5组
,第5组 ,然后绘制成如图所示的频率分布直方图,其中,第一组的频数为20.
,然后绘制成如图所示的频率分布直方图,其中,第一组的频数为20.
(1)求
 和
和 的值,并根据频率分布直方图估计这组数据的众数;
的值,并根据频率分布直方图估计这组数据的众数;(2)从第1,3,4组中用分层抽样的方法抽取6人,求第1,3,4组抽取的人数;
(3)在(2)抽取的6人中再随机抽取2人,求所抽取的2人来自同一个组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
, (其中
(其中 ,
, ,
, )的图象的两条相邻对称轴之间的距离为
)的图象的两条相邻对称轴之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为 .
.(1)求函数
 的解析式;
的解析式;(2)当
 时,求函数
时,求函数 的值域;
的值域;(3)若方程
 在
在 上有两个不相等的实数根
上有两个不相等的实数根 ,求
,求 的值.
的值.
相关试题

